Menu Close

0-1-ln-x-2-1-x-2-dx-pi-3-16-

Tinku Tara 0 Comments
Pin




Question Number 97369 by  M±th+et+s last updated on 07/Jun/20
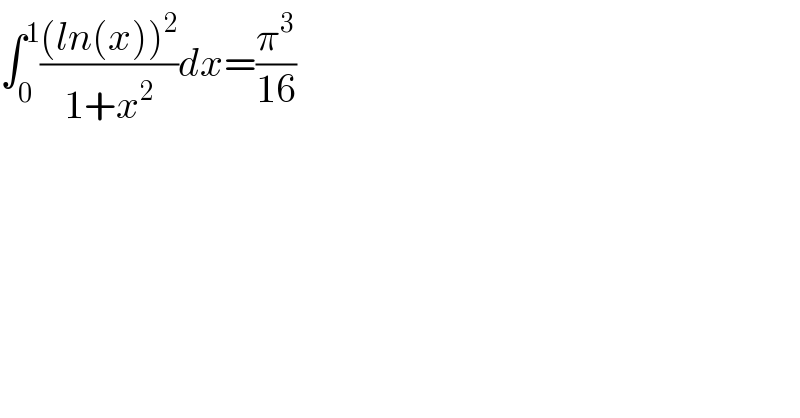
∫_0 ^1 (((ln(x))^2 )/(1+x^2 ))dx=(π^3 /(16))
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({ln}\left({x}\right)\right)^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}=\frac{\pi^{\mathrm{3}} }{\mathrm{16}} \\ $$
Answered by maths mind last updated on 07/Jun/20
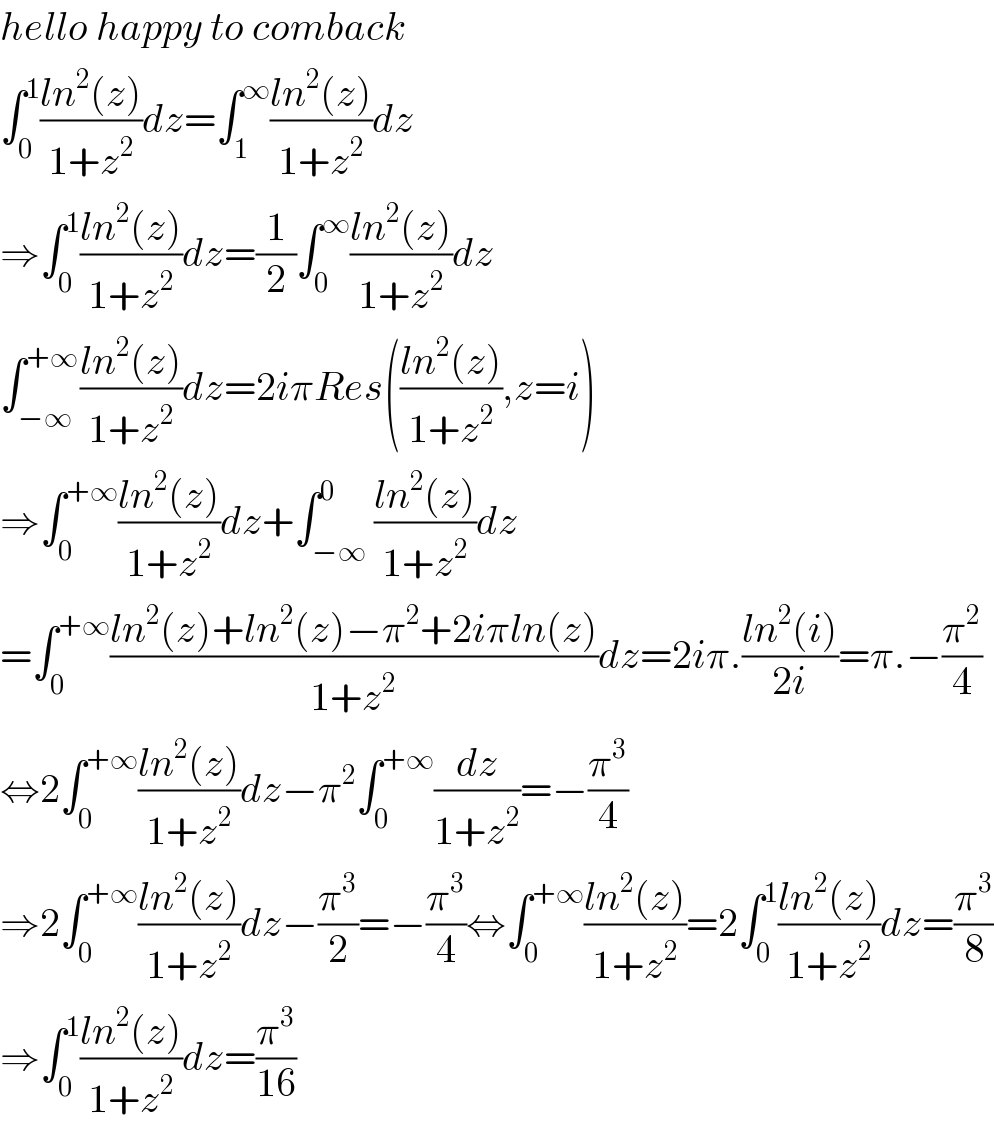
hello happy to comback ∫_0 ^1 ((ln^2 (z))/(1+z^2 ))dz=∫_1 ^∞ ((ln^2 (z))/(1+z^2 ))dz ⇒∫_0 ^1 ((ln^2 (z))/(1+z^2 ))dz=(1/2)∫_0 ^∞ ((ln^2 (z))/(1+z^2 ))dz ∫_(−∞) ^(+∞) ((ln^2 (z))/(1+z^2 ))dz=2iπRes(((ln^2 (z))/(1+z^2 )),z=i) ⇒∫_0 ^(+∞) ((ln^2 (z))/(1+z^2 ))dz+∫_(−∞) ^0 ((ln^2 (z))/(1+z^2 ))dz =∫_0 ^(+∞) ((ln^2 (z)+ln^2 (z)−π^2 +2iπln(z))/(1+z^2 ))dz=2iπ.((ln^2 (i))/(2i))=π.−(π^2 /4) ⇔2∫_0 ^(+∞) ((ln^2 (z))/(1+z^2 ))dz−π^2 ∫_0 ^(+∞) (dz/(1+z^2 ))=−(π^3 /4) ⇒2∫_0 ^(+∞) ((ln^2 (z))/(1+z^2 ))dz−(π^3 /2)=−(π^3 /4)⇔∫_0 ^(+∞) ((ln^2 (z))/(1+z^2 ))=2∫_0 ^1 ((ln^2 (z))/(1+z^2 ))dz=(π^3 /8) ⇒∫_0 ^1 ((ln^2 (z))/(1+z^2 ))dz=(π^3 /(16))
$${hello}\:{happy}\:{to}\:{comback}\: \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}=\int_{\mathrm{1}} ^{\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz} \\ $$$$\int_{−\infty} ^{+\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}=\mathrm{2}{i}\pi{Res}\left(\frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} },{z}={i}\right) \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}+\int_{−\infty} ^{\mathrm{0}} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)+{ln}^{\mathrm{2}} \left({z}\right)−\pi^{\mathrm{2}} +\mathrm{2}{i}\pi{ln}\left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}=\mathrm{2}{i}\pi.\frac{{ln}^{\mathrm{2}} \left({i}\right)}{\mathrm{2}{i}}=\pi.−\frac{\pi^{\mathrm{2}} }{\mathrm{4}} \\ $$$$\Leftrightarrow\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}−\pi^{\mathrm{2}} \int_{\mathrm{0}} ^{+\infty} \frac{{dz}}{\mathrm{1}+{z}^{\mathrm{2}} }=−\frac{\pi^{\mathrm{3}} }{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}−\frac{\pi^{\mathrm{3}} }{\mathrm{2}}=−\frac{\pi^{\mathrm{3}} }{\mathrm{4}}\Leftrightarrow\int_{\mathrm{0}} ^{+\infty} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }=\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}=\frac{\pi^{\mathrm{3}} }{\mathrm{8}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}^{\mathrm{2}} \left({z}\right)}{\mathrm{1}+{z}^{\mathrm{2}} }{dz}=\frac{\pi^{\mathrm{3}} }{\mathrm{16}} \\ $$
Commented by  M±th+et+s last updated on 07/Jun/20
how are you sir wellllllcomeeeee back very happy to see you again
$${how}\:{are}\:{you}\:{sir}\:{wellllllcomeeeee}\:{back} \\ $$$${very}\:{happy}\:{to}\:{see}\:{you}\:{again} \\ $$
Commented by maths mind last updated on 07/Jun/20
im fin thanx i hop you too
$${im}\:{fin}\:{thanx}\:{i}\:{hop}\:{you}\:{too} \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *