Question Number 84165 by M±th+et£s last updated on 10/Mar/20
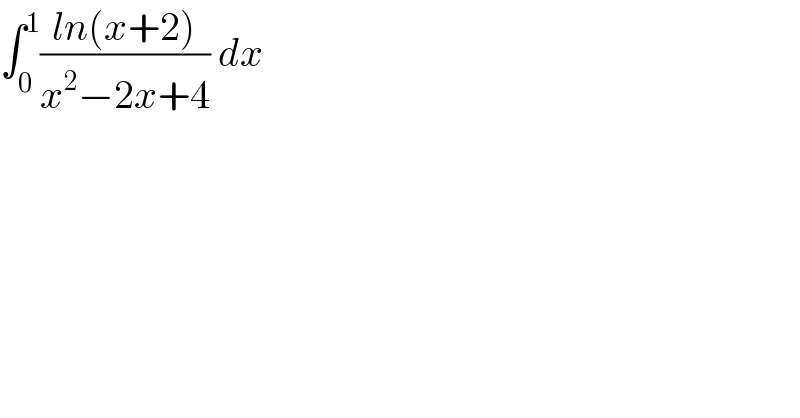
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}+\mathrm{2}\right)}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}}\:{dx} \\ $$
Commented by mathmax by abdo last updated on 10/Mar/20
![I =∫_0 ^1 ((ln(x+2))/(x^2 −2x+4))dx ⇒I=_(x+2=t) ∫_2 ^3 ((ln(t))/((t−2)^2 −2(t−2)+4))dt =∫_2 ^3 ((ln(t)dt)/(t^2 −4t+4−2t+8)) =∫_2 ^3 ((ln(t))/(t^2 −6t+12))dt =∫_2 ^3 ((ln(t))/(t^2 −6t +9 +12−9))dt =∫_2 ^3 ((ln(t))/((t−3)^2 +3))dt =_(3−t=(√3)u) − ∫_(1/( (√3))) ^0 ((ln(3−(√3)u))/(3(1+u^2 )))(√3)du =(1/( (√3)))∫_0 ^(1/( (√3))) ((ln(3−(√3)u))/(1+u^2 ))du =(1/( (√3)))∫_0 ^(1/( (√3))) ((ln(3)+ln(1−(1/( (√3)))u))/(1+u^2 ))du =((ln(3))/( (√3)))arctan((1/( (√3)))) +(1/( (√3)))∫_0 ^(1/( (√3))) ((ln(1−(1/( (√3)))u))/(1+u^2 ))du let f(a) =∫_0 ^(1/( (√3))) ((ln(1−au))/(1+u^2 ))du with ∣a∣<1 f^′ (a) =∫_0 ^(1/( (√3))) ((−u)/((1−au)(u^2 +1)))du =∫_0 ^(1/( (√3))) (u/((au−1)(u^2 +1)))du let decompose F(u) =(u/((au−1)(u^2 +1))) ⇒ F(u)=(α/(au−1)) +((βu +λ)/(u^(2 ) +1)) α =(1/(a((1/a^2 )+1))) =(1/((1/a)+a)) =(a/(1+a^2 )) lim_(u→+∞) uF(u)=0 =(α/a) +β ⇒β =−(1/(1+a^2 )) F(0)=0 =−α +λ ⇒λ =(a/(1+a^2 )) ⇒ F(u)=(a/((1+a^2 )(au−1))) +((−(1/(1+a^2 ))u +(a/(1+a^2 )))/(1+u^2 )) ⇒ f^′ (a) =(a/((1+a^2 )))∫_0 ^(1/( (√3))) (du/(au−1)) −(1/(2(1+a^2 )))∫_0 ^(1/( (√3))) ((2u−2a)/(u^2 +1))du =(1/(1+a^2 ))[ln∣au−1∣]_0 ^(1/( (√3))) −(1/(2(1+a^2 )))[ln(u^2 +1)]_0 ^(1/( (√3))) +(a/(a^2 +1)) arctan((1/( (√3)))) =(1/(1+a^2 ))ln∣(a/( (√3)))−1∣−(1/(2(a^2 +1)))ln((4/3)) +(a/(a^2 +1))×(π/6) ....be continued...](https://www.tinkutara.com/question/Q84181.png)
$${I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{ln}\left({x}+\mathrm{2}\right)}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}}{dx}\:\Rightarrow{I}=_{{x}+\mathrm{2}={t}} \:\:\int_{\mathrm{2}} ^{\mathrm{3}} \:\frac{{ln}\left({t}\right)}{\left({t}−\mathrm{2}\right)^{\mathrm{2}} −\mathrm{2}\left({t}−\mathrm{2}\right)+\mathrm{4}}{dt} \\ $$$$=\int_{\mathrm{2}} ^{\mathrm{3}} \:\frac{{ln}\left({t}\right){dt}}{{t}^{\mathrm{2}} −\mathrm{4}{t}+\mathrm{4}−\mathrm{2}{t}+\mathrm{8}}\:=\int_{\mathrm{2}} ^{\mathrm{3}} \:\frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} −\mathrm{6}{t}+\mathrm{12}}{dt} \\ $$$$=\int_{\mathrm{2}} ^{\mathrm{3}} \:\frac{{ln}\left({t}\right)}{{t}^{\mathrm{2}} −\mathrm{6}{t}\:+\mathrm{9}\:+\mathrm{12}−\mathrm{9}}{dt}\:=\int_{\mathrm{2}} ^{\mathrm{3}} \:\frac{{ln}\left({t}\right)}{\left({t}−\mathrm{3}\right)^{\mathrm{2}} \:+\mathrm{3}}{dt} \\ $$$$=_{\mathrm{3}−{t}=\sqrt{\mathrm{3}}{u}} \:\:\:−\:\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\mathrm{0}} \:\:\frac{{ln}\left(\mathrm{3}−\sqrt{\mathrm{3}}{u}\right)}{\mathrm{3}\left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\sqrt{\mathrm{3}}{du}\:=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\:\frac{{ln}\left(\mathrm{3}−\sqrt{\mathrm{3}}{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\frac{{ln}\left(\mathrm{3}\right)+{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$$=\frac{{ln}\left(\mathrm{3}\right)}{\:\sqrt{\mathrm{3}}}{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)\:+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\frac{{ln}\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}{u}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du} \\ $$$${let}\:{f}\left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\frac{{ln}\left(\mathrm{1}−{au}\right)}{\mathrm{1}+{u}^{\mathrm{2}} }{du}\:\:{with}\:\mid{a}\mid<\mathrm{1} \\ $$$${f}^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\frac{−{u}}{\left(\mathrm{1}−{au}\right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}{du}\:=\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\:\frac{{u}}{\left({au}−\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}{du} \\ $$$${let}\:{decompose}\:{F}\left({u}\right)\:=\frac{{u}}{\left({au}−\mathrm{1}\right)\left({u}^{\mathrm{2}} \:+\mathrm{1}\right)}\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{\alpha}{{au}−\mathrm{1}}\:+\frac{\beta{u}\:+\lambda}{{u}^{\mathrm{2}\:} +\mathrm{1}} \\ $$$$\alpha\:=\frac{\mathrm{1}}{{a}\left(\frac{\mathrm{1}}{{a}^{\mathrm{2}} }+\mathrm{1}\right)}\:=\frac{\mathrm{1}}{\frac{\mathrm{1}}{{a}}+{a}}\:=\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$${lim}_{{u}\rightarrow+\infty} \:{uF}\left({u}\right)=\mathrm{0}\:=\frac{\alpha}{{a}}\:+\beta\:\Rightarrow\beta\:=−\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} } \\ $$$${F}\left(\mathrm{0}\right)=\mathrm{0}\:=−\alpha\:+\lambda\:\Rightarrow\lambda\:=\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} }\:\Rightarrow \\ $$$${F}\left({u}\right)=\frac{{a}}{\left(\mathrm{1}+{a}^{\mathrm{2}} \right)\left({au}−\mathrm{1}\right)}\:+\frac{−\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} }{u}\:+\frac{{a}}{\mathrm{1}+{a}^{\mathrm{2}} }}{\mathrm{1}+{u}^{\mathrm{2}} }\:\Rightarrow \\ $$$${f}^{'} \left({a}\right)\:=\frac{{a}}{\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\frac{{du}}{{au}−\mathrm{1}}\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}\int_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\:\:\frac{\mathrm{2}{u}−\mathrm{2}{a}}{{u}^{\mathrm{2}} \:+\mathrm{1}}{du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} }\left[{ln}\mid{au}−\mathrm{1}\mid\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\:\:\:\:−\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{a}^{\mathrm{2}} \right)}\left[{ln}\left({u}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{0}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} \:\:\:\:+\frac{{a}}{{a}^{\mathrm{2}} \:+\mathrm{1}}\:{arctan}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{a}^{\mathrm{2}} }{ln}\mid\frac{{a}}{\:\sqrt{\mathrm{3}}}−\mathrm{1}\mid−\frac{\mathrm{1}}{\mathrm{2}\left({a}^{\mathrm{2}} \:+\mathrm{1}\right)}{ln}\left(\frac{\mathrm{4}}{\mathrm{3}}\right)\:+\frac{{a}}{{a}^{\mathrm{2}} \:+\mathrm{1}}×\frac{\pi}{\mathrm{6}} \\ $$$$….{be}\:{continued}… \\ $$$$ \\ $$
Answered by mind is power last updated on 10/Mar/20

$$\int\frac{{ln}\left({x}+\mathrm{2}\right){dx}}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}}=\int\frac{{ln}\left({x}+\mathrm{2}\right){dx}}{\left({x}−\mathrm{1}−{i}\sqrt{\mathrm{3}}\right)\left({x}−\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)} \\ $$$$=\int\frac{{ln}\left({x}+\mathrm{2}\right){dx}}{\mathrm{2}{i}\sqrt{\mathrm{3}}\left({x}−\mathrm{1}−{i}\sqrt{\mathrm{3}}\right)}−\int\frac{{ln}\left({x}+\mathrm{2}\right){dx}}{\mathrm{2}{i}\sqrt{\mathrm{3}}\left({x}−\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)}…{A} \\ $$$$\int\frac{{ln}\left({x}+{a}\right)}{{x}+{b}}{dx} \\ $$$${t}={x}+{b}\Rightarrow\int\frac{{ln}\left({t}−{b}+{a}\right)}{{t}}{dt} \\ $$$$=\int\frac{{ln}\left(\left({a}−{b}\right)\left(\mathrm{1}−\frac{{t}}{{b}−{a}}\right)\right)}{{t}}{dt} \\ $$$$=\int\frac{{ln}\left({a}−{b}\right)}{{t}}{dt}+\int\frac{{ln}\left(\mathrm{1}−\frac{{t}}{{b}−{a}}\right){dt}}{{t}} \\ $$$${a}\neq{b}\Rightarrow \\ $$$${u}=\frac{{t}}{{b}−{a}},{in}\:\mathrm{2}{nd}\:{integral} \\ $$$${withe}\:{ln}\left({u}\right)={ln}\mid{u}\mid+{iarg}\left({u}\right)\:{ln}\:{over}\:\mathbb{C}−\left\{{D}\right\}\: \\ $$$$=\int\frac{{ln}\left({a}−{b}\right)}{{t}}{dt}+\int\frac{{ln}\left(\mathrm{1}−{u}\right)}{{u}}{du} \\ $$$$={ln}\left({a}−{b}\right){ln}\left({t}\right)−{Li}_{\mathrm{2}} \left({u}\right)+{c} \\ $$$$={ln}\left({a}−{b}\right){ln}\left({x}+{b}\right)−{Li}_{\mathrm{2}} \left(\frac{{x}+{b}}{{b}−{a}}\right)+{c} \\ $$$$ \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}.\left\{\int\frac{{ln}\left({x}+\mathrm{2}\right){dx}}{{x}+\left(−\mathrm{1}−{i}\sqrt{\mathrm{3}}\right)}−\int\frac{{ln}\left({x}+\mathrm{2}\right){dx}}{{x}+\left(−\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)}\right\} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}{i}\sqrt{\mathrm{3}}}\left\{{ln}\left(\mathrm{3}+{i}\sqrt{\mathrm{3}}\right){ln}\left({x}−\mathrm{1}−{i}\sqrt{\mathrm{3}}\right)−{Li}_{\mathrm{2}} \left(\frac{{x}−\mathrm{1}−{i}\sqrt{\mathrm{3}}}{−\mathrm{3}−{i}\sqrt{\mathrm{3}}}\right)\right. \\ $$$$\left.−{ln}\left(\mathrm{3}−{i}\sqrt{\mathrm{3}}\right){ln}\left({x}−\mathrm{1}+{i}\sqrt{\mathrm{3}}\right)+{Li}_{\mathrm{2}} \left(\frac{{x}−\mathrm{1}+{i}\sqrt{\mathrm{3}}}{−\mathrm{3}+{i}\sqrt{\mathrm{3}}}\right)\right\}+{c}={f}\left({x}\right) \\ $$$${we}\:{get} \\ $$$${f}\left(\mathrm{1}\right)−{f}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}+\mathrm{2}\right)}{{x}^{\mathrm{2}} −\mathrm{2}{x}+\mathrm{4}}{dx}\:{long}\:{expression}\:{but}\: \\ $$$${not}\:{so}\:{hard} \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 10/Mar/20

$${thank}\:{you}\:{sir} \\ $$
