Question Number 153151 by puissant last updated on 05/Sep/21
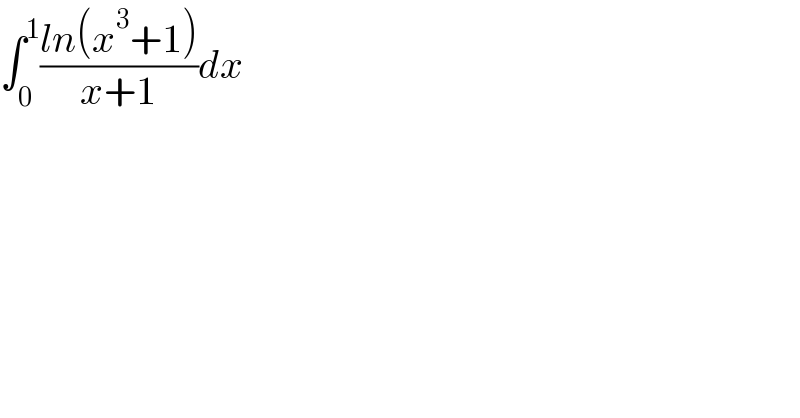
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}^{\mathrm{3}} +\mathrm{1}\right)}{{x}+\mathrm{1}}{dx} \\ $$
Answered by Ar Brandon last updated on 05/Sep/21

$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{ln}\left({x}^{\mathrm{3}} +\mathrm{1}\right)}{{x}+\mathrm{1}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}}\centerdot\frac{{x}^{\mathrm{3}{n}} }{\mathrm{1}+{x}}{dx} \\ $$$$\:\:=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{3}{n}} −{x}^{\mathrm{3}{n}+\mathrm{1}} }{\mathrm{1}−{x}^{\mathrm{2}} }{dx},\:{x}={u}^{\frac{\mathrm{1}}{\mathrm{2}}} \Rightarrow{dx}=\frac{\mathrm{1}}{\mathrm{2}}{u}^{−\frac{\mathrm{1}}{\mathrm{2}}} {du} \\ $$$$\:\:=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\frac{\mathrm{3}{n}−\mathrm{1}}{\mathrm{2}}} −{u}^{\frac{\mathrm{3}{n}}{\mathrm{2}}} }{\mathrm{1}−{u}}{du}=\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} }{\mathrm{2}{n}}\left(\psi\left(\frac{\mathrm{3}{n}}{\mathrm{2}}+\mathrm{1}\right)−\psi\left(\frac{\mathrm{3}{n}+\mathrm{1}}{\mathrm{2}}\right)\right) \\ $$
Commented by puissant last updated on 05/Sep/21

$${parfait}.. \\ $$
Answered by mindispower last updated on 05/Sep/21

$$={ln}\left({x}^{\mathrm{3}} +\mathrm{1}\right)={ln}\left(\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}^{\mathrm{2}} \left(\mathrm{2}\right)+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}^{\mathrm{2}} −{x}+\mathrm{1}\right)}{{x}+\mathrm{1}}{dx} \\ $$$$=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}^{\mathrm{2}} −{x}+\mathrm{1}} \\ $$$$=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{2}{x}−\mathrm{1}\right){ln}\left(\mathrm{1}+{x}\right)}{\left({x}−{j}\right)\left({x}−\overset{−} {{j}}\right)}{dx} \\ $$$$\frac{\mathrm{2}{x}−\mathrm{1}}{\left({x}−\boldsymbol{{j}}\right)\left(\boldsymbol{{x}}−\overset{−} {\boldsymbol{{j}}}\right)}=\frac{\mathrm{2}\boldsymbol{{j}}+\mathrm{1}}{{j}−\overset{−} {{j}}}.\frac{\mathrm{1}}{\boldsymbol{{x}}−\boldsymbol{{j}}}+\frac{\mathrm{2}\overset{−} {\boldsymbol{{j}}}−\mathrm{1}}{\overset{−} {{j}}−{j}}.\frac{\mathrm{1}}{\boldsymbol{{x}}−\overset{−} {\boldsymbol{{j}}}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{{x}+{a}}{dx} \\ $$$${x}+{a}={u} \\ $$$$=\int_{{a}} ^{{a}+\mathrm{1}} \frac{\left.{ln}\left(\mathrm{1}−{a}+{u}\right)\right)}{{u}}{du} \\ $$$${u}=\left({a}−\mathrm{1}\right){t},\forall{a}#\mathrm{1} \\ $$$$=\int_{−\frac{{a}}{\mathrm{1}−{a}}} ^{−\frac{{a}+\mathrm{1}}{\mathrm{1}−{a}}} \frac{{ln}\left(\mathrm{1}−{a}\right)+{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$$={ln}\left(\mathrm{1}−{a}\right)\left({ln}\left(\frac{{a}+\mathrm{1}}{{a}−\mathrm{1}}\right)−{ln}\left(\frac{{a}}{{a}−\mathrm{1}}\right)\right),\forall{a}\in{C}−\left(\mathrm{1},−\mathrm{1},\mathrm{0}\right) \\ $$$$−\int_{\mathrm{1}+\frac{\mathrm{2}}{{a}−\mathrm{1}}} ^{\mathrm{1}+\frac{\mathrm{1}}{{a}−\mathrm{1}}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt}={Li}_{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{1}}{{a}−\mathrm{1}}\right)−{Li}_{\mathrm{2}} \left(\mathrm{1}+\frac{\mathrm{2}}{{a}−\mathrm{1}}\right)'\forall\left(\frac{\mathrm{1}}{{a}−\mathrm{1}}\&\frac{\mathrm{2}}{{a}−\mathrm{1}}\right)\in{C}−\left[\mathrm{1},+\infty\left[\right.\right. \\ $$$${replac}\:{a}\:{by}\:{j}\:{and}\:\overset{−} {{j}}\:{we}\:{get}\:{close}\:{form} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by puissant last updated on 05/Sep/21

$${Sir}\:{mindispower},\:{you}\:{are}\:{a}\:{boss}\:!! \\ $$
Commented by mindispower last updated on 07/Sep/21

$${withe}\:{pleasur} \\ $$
