Question Number 162243 by cortano last updated on 28/Dec/21
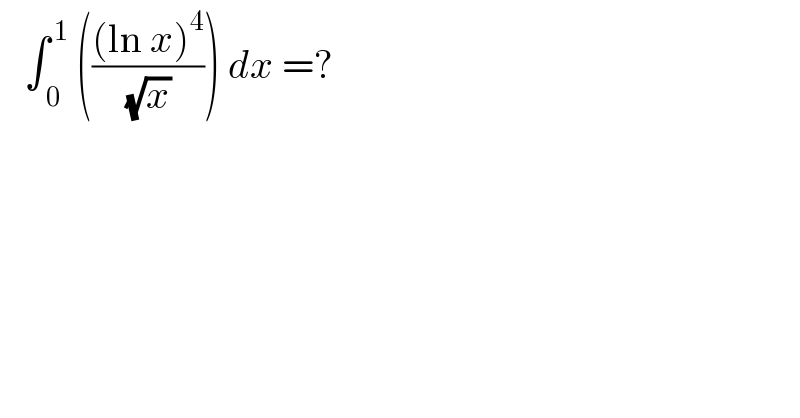
$$\:\:\:\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\left(\frac{\left(\mathrm{ln}\:{x}\right)^{\mathrm{4}} }{\:\sqrt{{x}}\:}\right)\:{dx}\:=? \\ $$
Answered by aleks041103 last updated on 28/Dec/21
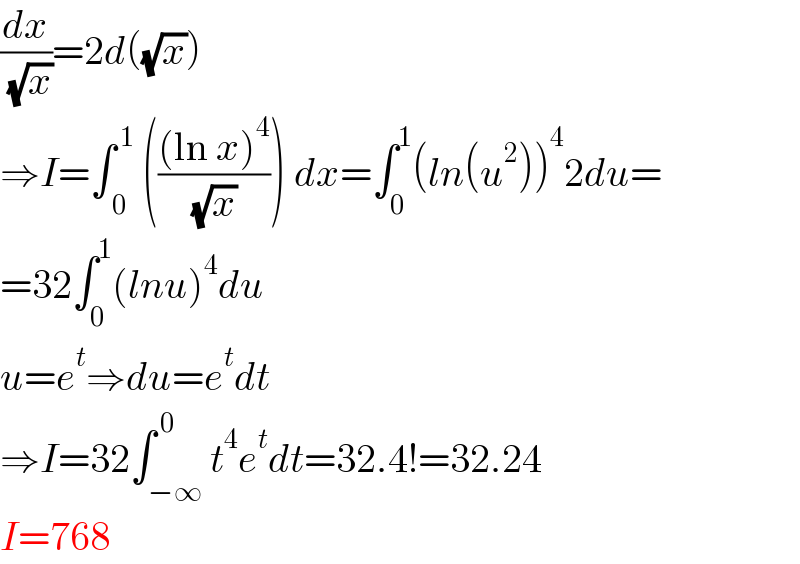
$$\frac{{dx}}{\:\sqrt{{x}}}=\mathrm{2}{d}\left(\sqrt{{x}}\right) \\ $$$$\Rightarrow{I}=\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\left(\frac{\left(\mathrm{ln}\:{x}\right)^{\mathrm{4}} }{\:\sqrt{{x}}\:}\right)\:{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \left({ln}\left({u}^{\mathrm{2}} \right)\right)^{\mathrm{4}} \mathrm{2}{du}= \\ $$$$=\mathrm{32}\int_{\mathrm{0}} ^{\mathrm{1}} \left({lnu}\right)^{\mathrm{4}} {du} \\ $$$${u}={e}^{{t}} \Rightarrow{du}={e}^{{t}} {dt} \\ $$$$\Rightarrow{I}=\mathrm{32}\int_{−\infty} ^{\:\mathrm{0}} {t}^{\mathrm{4}} {e}^{{t}} {dt}=\mathrm{32}.\mathrm{4}!=\mathrm{32}.\mathrm{24} \\ $$$${I}=\mathrm{768} \\ $$
Commented by aleks041103 last updated on 28/Dec/21
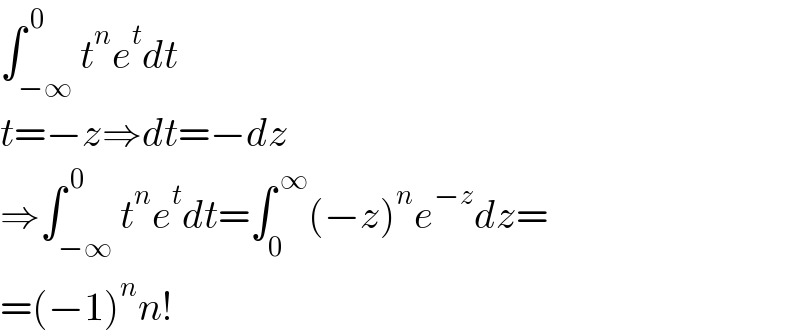
$$\int_{−\infty} ^{\:\mathrm{0}} {t}^{{n}} {e}^{{t}} {dt} \\ $$$${t}=−{z}\Rightarrow{dt}=−{dz} \\ $$$$\Rightarrow\int_{−\infty} ^{\:\mathrm{0}} {t}^{{n}} {e}^{{t}} {dt}=\int_{\mathrm{0}} ^{\:\infty} \left(−{z}\right)^{{n}} {e}^{−{z}} {dz}= \\ $$$$=\left(−\mathrm{1}\right)^{{n}} {n}! \\ $$
Answered by phanphuoc last updated on 28/Dec/21
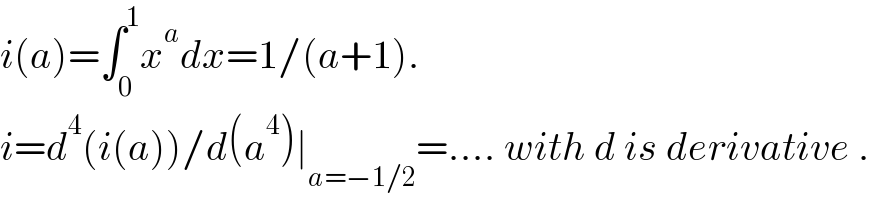
$${i}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} {dx}=\mathrm{1}/\left({a}+\mathrm{1}\right). \\ $$$${i}={d}^{\mathrm{4}} \left({i}\left({a}\right)\right)/{d}\left({a}^{\mathrm{4}} \right)\mid_{{a}=−\mathrm{1}/\mathrm{2}} =….\:{with}\:{d}\:{is}\:{derivative}\:. \\ $$
