Question Number 97235 by bobhans last updated on 07/Jun/20
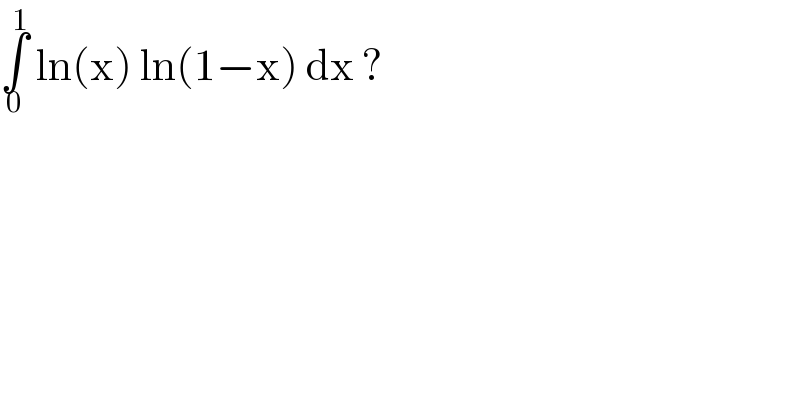
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{ln}\left(\mathrm{x}\right)\:\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\:\mathrm{dx}\:?\: \\ $$
Answered by abdomathmax last updated on 07/Jun/20
![I =∫_0 ^1 lnxln(1−x)dx we have for ∣x∣<1 (d/dx)ln(1−x) =((−1)/(1−x)) =−Σ_(n=0) ^∞ x^n ⇒ ln(1−x) =−Σ_(n=0) ^∞ (x^(n+1) /(n+1)) =−Σ_(n=1) ^∞ (x^n /n) ⇒ I =−∫_0 ^1 ln(x)(Σ_(n=1) ^∞ (x^n /n)) =−Σ_(n=1) ^∞ (1/n) ∫_0 ^1 x^n ln(x)dx by parts A_n =∫_0 ^1 x^n ln(x)dx =[(x^(n+1) /(n+1))ln(x)]_0 ^1 −∫_0 ^1 (x^(n+1) /(n+1))(dx/x) =−(1/(n+1)) ∫_0 ^(1 ) x^n dx =−(1/((n+1)^2 )) ⇒I =Σ_(n=1) ^∞ (1/(n(n+1)^2 )) let decompose F(x)=(1/(x(x+1)^2 )) ⇒ F(x) =(a/x) +(b/(x+1)) +(c/((x+1)^2 )) a =1 , c =−1 lim_(x→+∞) xF(x) =0 =a+b ⇒b=−1 ⇒ F(x) =(1/x)−(1/(x+1))−(1/((x+1)^2 )) ⇒ I =Σ_(n=1) ^∞ ((1/n)−(1/(n+1))) −Σ_(n=1) ^∞ (1/((n+1)^2 )) Σ_(n=1) ^∞ ((1/n)−(1/(n+1)))=lim_(n→∞) Σ_(k=1) ^n ((1/k)−(1/(k+1))) lim_(n→∞) (1−(1/(n+1))) =1 Σ_(n=1) ^∞ (1/((n+1)^2 )) =Σ_(n=2) ^∞ (1/n^2 ) =(π^2 /6)−1 ⇒ I =1−((π^2 /6)−1) =2−(π^2 /6)](https://www.tinkutara.com/question/Q97278.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{lnxln}\left(\mathrm{1}−\mathrm{x}\right)\mathrm{dx}\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{for}\:\mid\mathrm{x}\mid<\mathrm{1} \\ $$$$\frac{\mathrm{d}}{\mathrm{dx}}\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\:=\frac{−\mathrm{1}}{\mathrm{1}−\mathrm{x}}\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\mathrm{x}^{\mathrm{n}} \:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}−\mathrm{x}\right)\:=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\mathrm{I}\:\:=−\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{x}\right)\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{x}^{\mathrm{n}} }{\mathrm{n}}\right)\:=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\mathrm{by}\:\mathrm{parts}\:\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\mathrm{n}} \mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=\left[\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\mathrm{ln}\left(\mathrm{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\frac{\mathrm{dx}}{\mathrm{x}}\:=−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}\:} \mathrm{x}^{\mathrm{n}} \:\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow\mathrm{I}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{let}\:\mathrm{decompose}\:\mathrm{F}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{a}}{\mathrm{x}}\:+\frac{\mathrm{b}}{\mathrm{x}+\mathrm{1}}\:+\frac{\mathrm{c}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\mathrm{a}\:=\mathrm{1}\:,\:\mathrm{c}\:=−\mathrm{1} \\ $$$$\mathrm{lim}_{\mathrm{x}\rightarrow+\infty} \mathrm{xF}\left(\mathrm{x}\right)\:=\mathrm{0}\:=\mathrm{a}+\mathrm{b}\:\Rightarrow\mathrm{b}=−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{F}\left(\mathrm{x}\right)\:=\frac{\mathrm{1}}{\mathrm{x}}−\frac{\mathrm{1}}{\mathrm{x}+\mathrm{1}}−\frac{\mathrm{1}}{\left(\mathrm{x}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{I}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)\:−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \left(\frac{\mathrm{1}}{\mathrm{n}}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)={lim}_{{n}\rightarrow\infty} \sum_{\mathrm{k}=\mathrm{1}} ^{\mathrm{n}} \left(\frac{\mathrm{1}}{\mathrm{k}}−\frac{\mathrm{1}}{\mathrm{k}+\mathrm{1}}\right) \\ $$$$\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{n}+\mathrm{1}}\right)\:=\mathrm{1} \\ $$$$\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\left(\mathrm{n}+\mathrm{1}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{2}} ^{\infty} \:\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} }\:=\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{1}−\left(\frac{\pi^{\mathrm{2}} }{\mathrm{6}}−\mathrm{1}\right)\:=\mathrm{2}−\frac{\pi^{\mathrm{2}} }{\mathrm{6}} \\ $$$$ \\ $$$$ \\ $$
Commented by bobhans last updated on 07/Jun/20

$$\mathrm{thank}\:\mathrm{you}.\:\mathrm{great} \\ $$
