Question Number 118246 by bemath last updated on 16/Oct/20
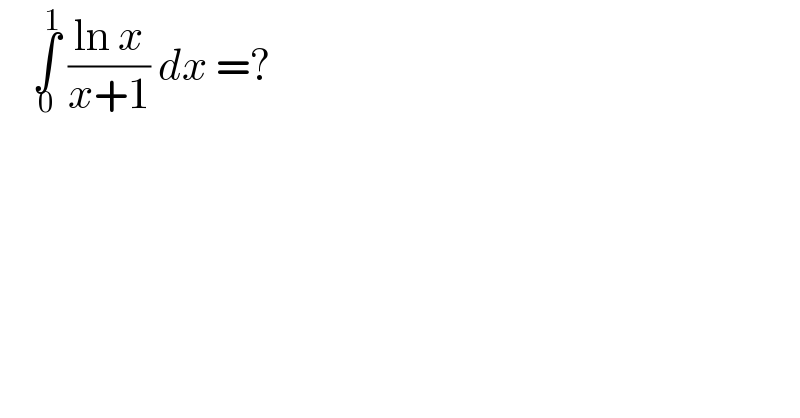
$$\:\:\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{ln}\:{x}}{{x}+\mathrm{1}}\:{dx}\:=? \\ $$
Answered by Dwaipayan Shikari last updated on 16/Oct/20
![∫_0 ^1 ((logx)/(x+1))dx=[log(x)log(x+1)]_0 ^1 −∫_0 ^1 (1/x)log(x+1) =0−∫_0 ^1 (−1)^(n+1) Σ_(n=1) ^∞ (x^(n−1) /n) =−Σ_(n=1) ^∞ (−1)^(n+1) (1/n^2 ) =−(π^2 /(12))](https://www.tinkutara.com/question/Q118257.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{logx}}{{x}+\mathrm{1}}{dx}=\left[{log}\left({x}\right){log}\left({x}+\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{{x}}{log}\left({x}+\mathrm{1}\right) \\ $$$$=\mathrm{0}−\int_{\mathrm{0}} ^{\mathrm{1}} \left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{x}^{{n}−\mathrm{1}} }{{n}} \\ $$$$=−\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}+\mathrm{1}} \frac{\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$=−\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$
