Menu Close

0-1-log-1-x-7-1-x-7-dx-

Tinku Tara 0 Comments
Pin




Question Number 162219 by mathlove last updated on 27/Dec/21
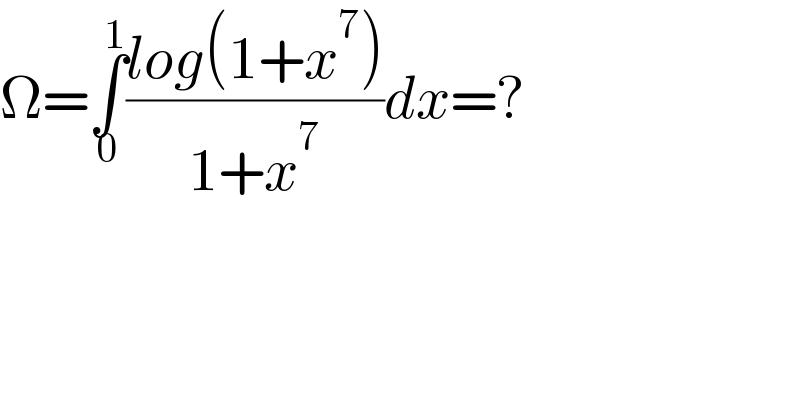
Ω=∫_0 ^1 ((log(1+x^7 ))/(1+x^7 ))dx=?
$$\Omega=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{log}\left(\mathrm{1}+{x}^{\mathrm{7}} \right)}{\mathrm{1}+{x}^{\mathrm{7}} }{dx}=? \\ $$
Answered by amin96 last updated on 27/Dec/21
x^7 =−t (dt/dx)=−7x^6 =−7t^(6/7) Ω=(1/7)∫_(−1) ^0 ((ln(1−t))/((1−t)t^(6/7) ))dt=−(1/7)Σ_(n=1) ^∞ H_n ∫_(−1) ^0 t^(n−(6/7)) dt= =−(1/7)Σ_(n=1) ^∞ H_n [(t^(n+(1/7)) /(n+(1/7)))]_(−1) ^0 =−(1/7)Σ_(n=1) ^∞ ((H_n (−1)^(n+(1/7)) )/((n+(1/7))))= =(1/7)Σ_(n=1) ^∞ ((H_n (−1)^n )/((n+(1/7))))=Σ_(n=1) ^∞ (((−1)^n H_n )/(7n+1))
$$\boldsymbol{{x}}^{\mathrm{7}} =−\boldsymbol{{t}}\:\:\:\:\frac{\boldsymbol{{dt}}}{\boldsymbol{{dx}}}=−\mathrm{7}\boldsymbol{{x}}^{\mathrm{6}} =−\mathrm{7}\boldsymbol{{t}}^{\frac{\mathrm{6}}{\mathrm{7}}} \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{7}}\int_{−\mathrm{1}} ^{\mathrm{0}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{\left(\mathrm{1}−{t}\right){t}^{\frac{\mathrm{6}}{\mathrm{7}}} }{dt}=−\frac{\mathrm{1}}{\mathrm{7}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \int_{−\mathrm{1}} ^{\mathrm{0}} {t}^{\boldsymbol{\mathrm{n}}−\frac{\mathrm{6}}{\mathrm{7}}} {dt}= \\ $$$$=−\frac{\mathrm{1}}{\mathrm{7}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \left[\frac{\boldsymbol{\mathrm{t}}^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{7}}} }{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{7}}}\right]_{−\mathrm{1}} ^{\mathrm{0}} =−\frac{\mathrm{1}}{\mathrm{7}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{7}}} }{\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{7}}\right)}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{7}}\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} \left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}} }{\left(\boldsymbol{\mathrm{n}}+\frac{\mathrm{1}}{\mathrm{7}}\right)}=\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\left(−\mathrm{1}\right)^{\boldsymbol{\mathrm{n}}} \boldsymbol{\mathrm{H}}_{\boldsymbol{\mathrm{n}}} }{\mathrm{7}\boldsymbol{\mathrm{n}}+\mathrm{1}} \\ $$
Answered by mindispower last updated on 30/Dec/21
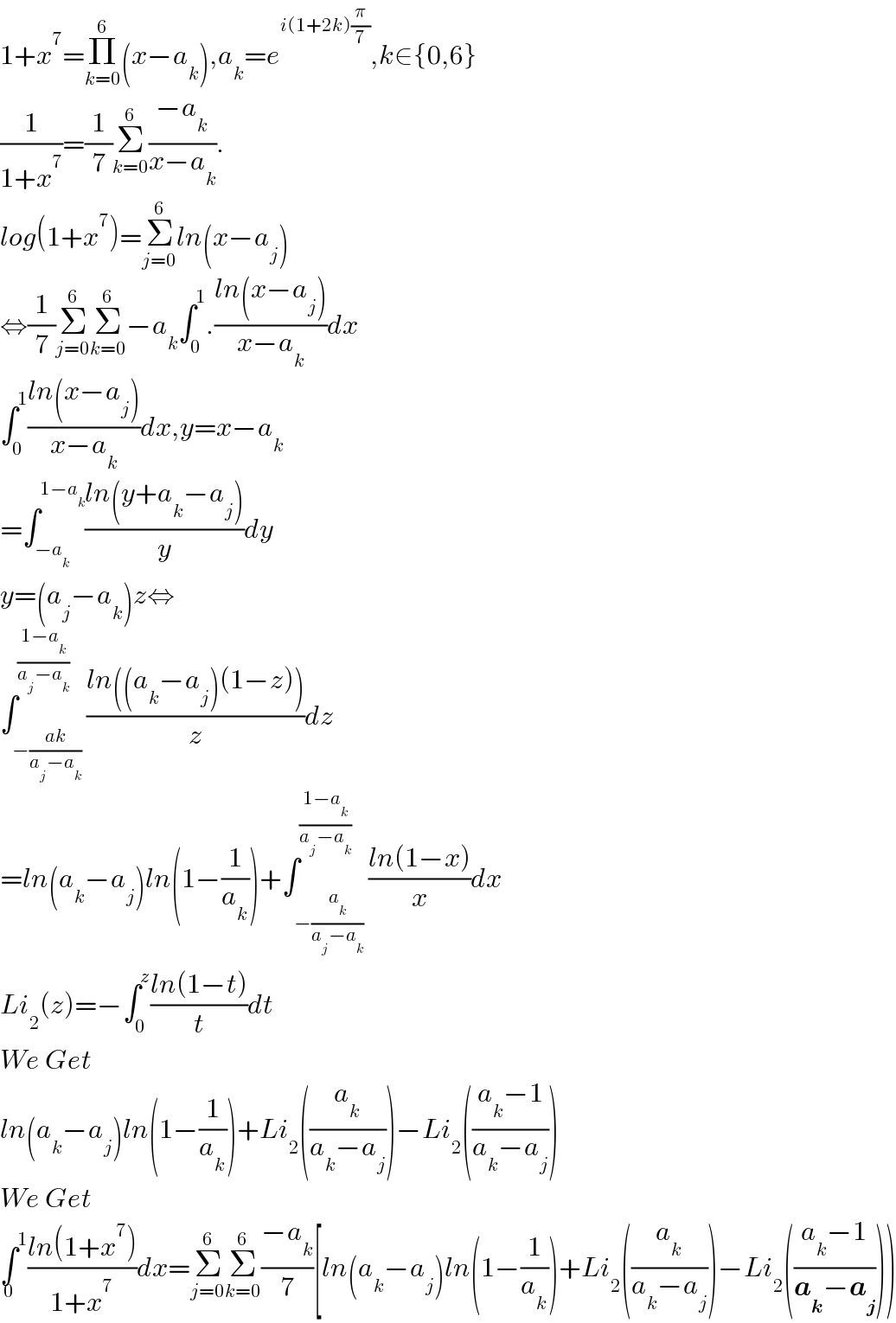
1+x^7 =Π_(k=0) ^6 (x−a_k ),a_k =e^(i(1+2k)(π/7)) ,k∈{0,6} (1/(1+x^7 ))=(1/7)Σ_(k=0) ^6 ((−a_k )/(x−a_k )). log(1+x^7 )=Σ_(j=0) ^6 ln(x−a_j ) ⇔(1/7)Σ_(j=0) ^6 Σ_(k=0) ^6 −a_k ∫_0 ^1 .((ln(x−a_j ))/(x−a_k ))dx ∫_0 ^1 ((ln(x−a_j ))/(x−a_k ))dx,y=x−a_k =∫_(−a_k ) ^(1−a_k ) ((ln(y+a_k −a_j ))/y)dy y=(a_j −a_k )z⇔ ∫_(−((ak)/(a_j −a_k ))) ^((1−a_k )/(a_j −a_k )) ((ln((a_k −a_j )(1−z)))/z)dz =ln(a_k −a_j )ln(1−(1/a_k ))+∫_(−(a_k /(a_j −a_k ))) ^((1−a_k )/(a_j −a_k )) ((ln(1−x))/x)dx Li_2 (z)=−∫_0 ^z ((ln(1−t))/t)dt We Get ln(a_k −a_j )ln(1−(1/a_k ))+Li_2 ((a_k /(a_k −a_j )))−Li_2 (((a_k −1)/(a_k −a_j ))) We Get ∫^1 _0 ((ln(1+x^7 ))/(1+x^7 ))dx=Σ_(j=0) ^6 Σ_(k=0) ^6 ((−a_k )/7)[ln(a_k −a_j )ln(1−(1/a_k ))+Li_2 ((a_k /(a_k −a_j )))−Li_2 (((a_k −1)/(a_k −a_j ))))
$$\mathrm{1}+{x}^{\mathrm{7}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\prod}}\left({x}−{a}_{{k}} \right),{a}_{{k}} ={e}^{{i}\left(\mathrm{1}+\mathrm{2}{k}\right)\frac{\pi}{\mathrm{7}}} ,{k}\in\left\{\mathrm{0},\mathrm{6}\right\} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{7}} }=\frac{\mathrm{1}}{\mathrm{7}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}\frac{−{a}_{{k}} }{{x}−{a}_{{k}} }. \\ $$$${log}\left(\mathrm{1}+{x}^{\mathrm{7}} \right)=\underset{{j}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}{ln}\left({x}−{a}_{{j}} \right) \\ $$$$\Leftrightarrow\frac{\mathrm{1}}{\mathrm{7}}\underset{{j}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}−{a}_{{k}} \int_{\mathrm{0}} ^{\mathrm{1}} .\frac{{ln}\left({x}−{a}_{{j}} \right)}{{x}−{a}_{{k}} }{dx} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left({x}−{a}_{{j}} \right)}{{x}−{a}_{{k}} }{dx},{y}={x}−{a}_{{k}} \\ $$$$=\int_{−{a}_{{k}} } ^{\mathrm{1}−{a}_{{k}} } \frac{{ln}\left({y}+{a}_{{k}} −{a}_{{j}} \right)}{{y}}{dy} \\ $$$${y}=\left({a}_{{j}} −{a}_{{k}} \right){z}\Leftrightarrow \\ $$$$\int_{−\frac{{ak}}{{a}_{{j}} −{a}_{{k}} }} ^{\frac{\mathrm{1}−{a}_{{k}} }{{a}_{{j}} −{a}_{{k}} }} \frac{{ln}\left(\left({a}_{{k}} −{a}_{{j}} \right)\left(\mathrm{1}−{z}\right)\right)}{{z}}{dz} \\ $$$$={ln}\left({a}_{{k}} −{a}_{{j}} \right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{a}_{{k}} }\right)+\int_{−\frac{{a}_{{k}} }{{a}_{{j}} −{a}_{{k}} }} ^{\frac{\mathrm{1}−{a}_{{k}} }{{a}_{{j}} −{a}_{{k}} }} \frac{{ln}\left(\mathrm{1}−{x}\right)}{{x}}{dx} \\ $$$${Li}_{\mathrm{2}} \left({z}\right)=−\int_{\mathrm{0}} ^{{z}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{{t}}{dt} \\ $$$${We}\:{Get} \\ $$$${ln}\left({a}_{{k}} −{a}_{{j}} \right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{a}_{{k}} }\right)+{Li}_{\mathrm{2}} \left(\frac{{a}_{{k}} }{{a}_{{k}} −{a}_{{j}} }\right)−{Li}_{\mathrm{2}} \left(\frac{{a}_{{k}} −\mathrm{1}}{{a}_{{k}} −{a}_{{j}} }\right) \\ $$$${We}\:{Get} \\ $$$$\underset{\mathrm{0}} {\int}^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}^{\mathrm{7}} \right)}{\mathrm{1}+{x}^{\mathrm{7}} }{dx}=\underset{{j}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{6}} {\sum}}\frac{−{a}_{{k}} }{\mathrm{7}}\left[{ln}\left({a}_{{k}} −{a}_{{j}} \right){ln}\left(\mathrm{1}−\frac{\mathrm{1}}{{a}_{{k}} }\right)+{Li}_{\mathrm{2}} \left(\frac{{a}_{{k}} }{{a}_{{k}} −{a}_{{j}} }\right)−{Li}_{\mathrm{2}} \left(\frac{{a}_{{k}} −\mathrm{1}}{\boldsymbol{{a}}_{\boldsymbol{{k}}} −\boldsymbol{{a}}_{\boldsymbol{{j}}} }\right)\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *