Menu Close

0-1-log-1-x-x-2-x-3-x-4-dx-x-pi-2-15-

Tinku Tara 0 Comments
Pin




Question Number 104644 by Rohit@Thakur last updated on 22/Jul/20
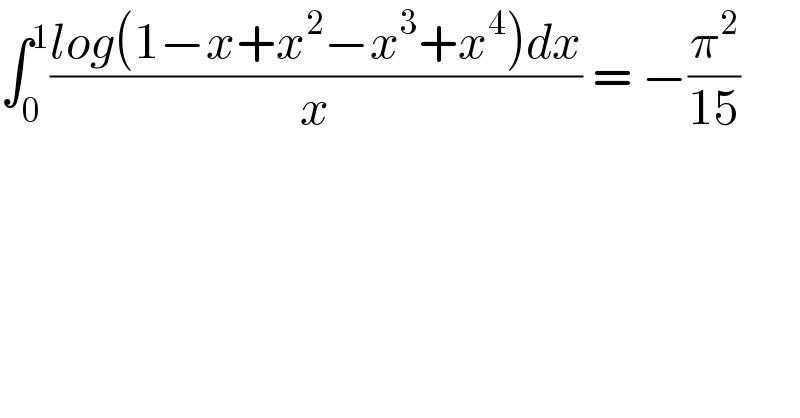
∫_0 ^1 ((log(1−x+x^2 −x^3 +x^4 )dx)/x) = −(π^2 /(15))
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{log}\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} −{x}^{\mathrm{3}} +{x}^{\mathrm{4}} \right){dx}}{{x}}\:=\:−\frac{\pi^{\mathrm{2}} }{\mathrm{15}} \\ $$
Answered by mathmax by abdo last updated on 23/Jul/20
I =∫_0 ^1 ((ln(1−x+x^2 −x^3 +x^4 ))/x)dx ⇒I =∫_0 ^1 ((ln(((1−(−x)^5 )/(1−(−x)))))/x)dx =∫_0 ^1 ((ln(1+x^5 )−ln(1+x))/x)dx =∫_0 ^1 ((ln(1+x^5 ))/x)dx−∫_0 ^1 ((ln(1+x))/x)dx we have ln^′ (1+u) =(1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n for ∣u∣<1 ⇒ ln(1+u)=Σ_(n=0) ^∞ (((−1)^n u^(n+1) )/(n+1)) +c(c=0) =Σ_(n=1) ^∞ (((−1)^(n−1) u^n )/n) ⇒ ((ln(1+x))/x) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) x^(n−1) ⇒∫_0 ^(1 ) ((ln(1+x))/x)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/n^2 ) =−Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =−δ(2) =−(2^(1−2) −1)ξ(2) =−(−(1/2))×(π^2 /6) =(π^2 /(12)) ln(1+x^5 ) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) x^(5n) ⇒((ln(1+x^5 ))/x) =Σ_(n=1) ^∞ (((−1)^(n−1) )/n) x^(5n−1) ⇒ ∫_0 ^1 ((ln(1+x^5 ))/x)dx =Σ_(n=1) ^∞ (((−1)^(n−1) )/(n(5n))) =−(1/5) Σ_(n=1) ^∞ (((−1)^n )/n^2 ) =(1/5)×(π^2 /(12)) =(π^2 /(60)) ⇒ I =(π^2 /(60))−(π^2 /(12)) =((1/(60))−(1/(12)))π^2 =((1−5)/(60))×π^2 =−((4π^2 )/(60)) =−(π^2 /(15)) the result is proved.
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}−\mathrm{x}+\mathrm{x}^{\mathrm{2}} −\mathrm{x}^{\mathrm{3}} \:+\mathrm{x}^{\mathrm{4}} \right)}{\mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\frac{\mathrm{1}−\left(−\mathrm{x}\right)^{\mathrm{5}} }{\mathrm{1}−\left(−\mathrm{x}\right)}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)−\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)}{\mathrm{x}}\mathrm{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{we}\:\mathrm{have}\:\mathrm{ln}^{'} \left(\mathrm{1}+\mathrm{u}\right)\:=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}} \:\:\:\mathrm{for}\:\mid\mathrm{u}\mid<\mathrm{1}\:\Rightarrow \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{u}\right)=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}+\mathrm{1}} }{\mathrm{n}+\mathrm{1}}\:+\mathrm{c}\left(\mathrm{c}=\mathrm{0}\right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \mathrm{u}^{\mathrm{n}} }{\mathrm{n}}\:\Rightarrow \\ $$$$\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\mathrm{x}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}\:} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}^{\mathrm{2}} } \\ $$$$=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\:=−\delta\left(\mathrm{2}\right)\:=−\left(\mathrm{2}^{\mathrm{1}−\mathrm{2}} −\mathrm{1}\right)\xi\left(\mathrm{2}\right)\:=−\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)×\frac{\pi^{\mathrm{2}} }{\mathrm{6}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{12}} \\ $$$$\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\mathrm{x}^{\mathrm{5n}} \:\Rightarrow\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)}{\mathrm{x}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}}\:\mathrm{x}^{\mathrm{5n}−\mathrm{1}} \:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{ln}\left(\mathrm{1}+\mathrm{x}^{\mathrm{5}} \right)}{\mathrm{x}}\mathrm{dx}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\mathrm{n}\left(\mathrm{5n}\right)}\:=−\frac{\mathrm{1}}{\mathrm{5}}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\mathrm{n}^{\mathrm{2}} }\:=\frac{\mathrm{1}}{\mathrm{5}}×\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{60}} \\ $$$$\Rightarrow\:\mathrm{I}\:=\frac{\pi^{\mathrm{2}} }{\mathrm{60}}−\frac{\pi^{\mathrm{2}} }{\mathrm{12}}\:=\left(\frac{\mathrm{1}}{\mathrm{60}}−\frac{\mathrm{1}}{\mathrm{12}}\right)\pi^{\mathrm{2}} \:=\frac{\mathrm{1}−\mathrm{5}}{\mathrm{60}}×\pi^{\mathrm{2}} \:=−\frac{\mathrm{4}\pi^{\mathrm{2}} }{\mathrm{60}}\:=−\frac{\pi^{\mathrm{2}} }{\mathrm{15}} \\ $$$$\mathrm{the}\:\mathrm{result}\:\mathrm{is}\:\mathrm{proved}. \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *