Question Number 105940 by Dwaipayan Shikari last updated on 01/Aug/20
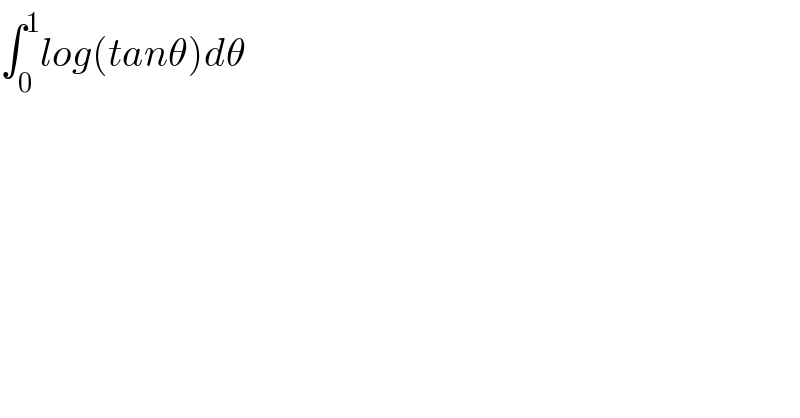
$$\int_{\mathrm{0}} ^{\mathrm{1}} {log}\left({tan}\theta\right){d}\theta \\ $$
Answered by mathmax by abdo last updated on 01/Aug/20
![A =∫_0 ^1 ln(tanθ)dθ by parts A = [θln(tanθ)]_0 ^1 −∫_0 ^1 θ×((1+tan^2 θ)/(tanθ)) dθ =ln((π/4))−∫_0 ^1 θ{(1/(tanθ)) +tanθ}dθ changement tanθ =x give ∫_0 ^1 θ{(1/(tanθ)) +tanθ }dθ =∫_0 ^(tan(1)) arctanx{(1/x) +x}(dx/(1+x^2 )) =∫_0 ^(tan(1)) ((1+x^2 )/x) ×((arctanx)/(1+x^2 ))dx =∫_0 ^(tan(1)) ((arctan(x))/x)dx let f(a) =∫_0 ^(tan(1)) ((arctan(αx))/x)dx ⇒f^′ (a) =∫_0 ^(tan(1)) (x/((1+α^2 x^2 )x))dx =∫_0 ^(tan(1)) (dx/(1+α^2 x^2 )) =_(αx =z) ∫_0 ^(αtan(1)) (dz/(α(1+z^2 ))) =(1/α)[arctanz]_0 ^(αtan(1)) =((arctan(αtan(1)))/α) ⇒f(α) =∫_0 ^α ((arctan(utan(1)))/u) du + C and ∫_0 ^(tan(1)) ((arctanx)/x)dx =f(1) =∫_0 ^1 ((arctan(utan(1)))/u) du +C ..be continued...](https://www.tinkutara.com/question/Q105954.png)
$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{ln}\left(\mathrm{tan}\theta\right)\mathrm{d}\theta\:\:\mathrm{by}\:\mathrm{parts}\:\mathrm{A}\:=\:\left[\theta\mathrm{ln}\left(\mathrm{tan}\theta\right)\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \theta×\frac{\mathrm{1}+\mathrm{tan}^{\mathrm{2}} \theta}{\mathrm{tan}\theta}\:\mathrm{d}\theta \\ $$$$=\mathrm{ln}\left(\frac{\pi}{\mathrm{4}}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \theta\left\{\frac{\mathrm{1}}{\mathrm{tan}\theta}\:+\mathrm{tan}\theta\right\}\mathrm{d}\theta\:\:\:\mathrm{changement}\:\mathrm{tan}\theta\:=\mathrm{x}\:\mathrm{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \theta\left\{\frac{\mathrm{1}}{\mathrm{tan}\theta}\:+\mathrm{tan}\theta\:\right\}\mathrm{d}\theta\:=\int_{\mathrm{0}} ^{\mathrm{tan}\left(\mathrm{1}\right)} \:\mathrm{arctanx}\left\{\frac{\mathrm{1}}{\mathrm{x}}\:+\mathrm{x}\right\}\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{tan}\left(\mathrm{1}\right)} \:\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }{\mathrm{x}}\:×\frac{\mathrm{arctanx}}{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\mathrm{dx}\:\:=\int_{\mathrm{0}} ^{\mathrm{tan}\left(\mathrm{1}\right)} \:\frac{\mathrm{arctan}\left(\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx} \\ $$$$\mathrm{let}\:\mathrm{f}\left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{tan}\left(\mathrm{1}\right)} \:\frac{\mathrm{arctan}\left(\alpha\mathrm{x}\right)}{\mathrm{x}}\mathrm{dx}\:\Rightarrow\mathrm{f}^{'} \left(\mathrm{a}\right)\:=\int_{\mathrm{0}} ^{\mathrm{tan}\left(\mathrm{1}\right)} \:\frac{\mathrm{x}}{\left(\mathrm{1}+\alpha^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} \right)\mathrm{x}}\mathrm{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{tan}\left(\mathrm{1}\right)} \:\frac{\mathrm{dx}}{\mathrm{1}+\alpha^{\mathrm{2}} \mathrm{x}^{\mathrm{2}} }\:=_{\alpha\mathrm{x}\:=\mathrm{z}} \:\:\:\int_{\mathrm{0}} ^{\alpha\mathrm{tan}\left(\mathrm{1}\right)} \:\frac{\mathrm{dz}}{\alpha\left(\mathrm{1}+\mathrm{z}^{\mathrm{2}} \right)}\:=\frac{\mathrm{1}}{\alpha}\left[\mathrm{arctanz}\right]_{\mathrm{0}} ^{\alpha\mathrm{tan}\left(\mathrm{1}\right)} \\ $$$$=\frac{\mathrm{arctan}\left(\alpha\mathrm{tan}\left(\mathrm{1}\right)\right)}{\alpha}\:\Rightarrow\mathrm{f}\left(\alpha\right)\:=\int_{\mathrm{0}} ^{\alpha} \frac{\mathrm{arctan}\left(\mathrm{utan}\left(\mathrm{1}\right)\right)}{\mathrm{u}}\:\mathrm{du}\:+\:\mathrm{C} \\ $$$$\mathrm{and}\:\int_{\mathrm{0}} ^{\mathrm{tan}\left(\mathrm{1}\right)} \:\frac{\mathrm{arctanx}}{\mathrm{x}}\mathrm{dx}\:=\mathrm{f}\left(\mathrm{1}\right)\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{arctan}\left(\mathrm{utan}\left(\mathrm{1}\right)\right)}{\mathrm{u}}\:\mathrm{du}\:+\mathrm{C} \\ $$$$..\mathrm{be}\:\mathrm{continued}… \\ $$
