Question Number 173148 by JordanRoddy last updated on 07/Jul/22

$$ \\ $$$$ \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:^{\mathrm{n}} \sqrt{\mathrm{x}}\:\left(\mathrm{arcsin}\:\mathrm{x}\right)\:\mathrm{dx} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Answered by Mathspace last updated on 07/Jul/22
![I_n =∫_0 ^1 (^n (√x))arcsinx dx we do the changement arcsinx=t ⇒ x=sint and I_n =∫_0 ^(π/2) (sint)^(1/n) t cost dt =∫_0 ^(π/2) t(cost (sint)^(1/n) )dt =[(t/(1+(1/n)))(sint)^(1+(1/n)) ]_0 ^(π/2) −∫_0 ^(π/2) (n/(n+1))(sint)^(1+(1/n)) dt ((πn)/(2(n+1)))−(n/(n+1))∫_0 ^(π/2) (sint)^(1+(1/n)) dt we have ∫_0 ^(π/2) (cost)^(2p−1) .(sint)^(2q−1) dt =B(ρ,q)=((Γ(ρ).Γ(q))/(Γ(ρ+q))) ⇒ 2ρ−1=0 and 2q−1=1+(1/n) ⇒ρ=(1/2) and q=1+(1/(2n)) ∫_0 ^(π/2) (sint)^(1+(1/n)) dt=((Γ((1/2))Γ(1+(1/(2n))))/(2Γ((1/2)+1+(1/(2n))))) =((√π)/2)×((Γ(1+(1/(2n))))/(Γ((3/2)+(1/(2n))))) ⇒ I_n =((nπ)/(2(n+1)))−(n/(n+1)).((√π)/2)×((Γ(1+(1/(2n))))/(Γ((3/2)+(1/(2n)))))](https://www.tinkutara.com/question/Q173155.png)
$${I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \left(^{{n}} \sqrt{{x}}\right){arcsinx}\:{dx}\:{we}\:{do} \\ $$$${the}\:{changement}\:{arcsinx}={t}\:\Rightarrow \\ $$$${x}={sint}\:{and} \\ $$$${I}_{{n}} =\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sint}\right)^{\frac{\mathrm{1}}{{n}}} {t}\:{cost}\:{dt} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {t}\left({cost}\:\left({sint}\right)^{\frac{\mathrm{1}}{{n}}} \right){dt} \\ $$$$=\left[\frac{{t}}{\mathrm{1}+\frac{\mathrm{1}}{{n}}}\left({sint}\right)^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} \right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{n}}{{n}+\mathrm{1}}\left({sint}\right)^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} {dt} \\ $$$$\frac{\pi{n}}{\mathrm{2}\left({n}+\mathrm{1}\right)}−\frac{{n}}{{n}+\mathrm{1}}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sint}\right)^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} {dt} \\ $$$${we}\:{have}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({cost}\right)^{\mathrm{2}{p}−\mathrm{1}} .\left({sint}\right)^{\mathrm{2}{q}−\mathrm{1}} {dt} \\ $$$$={B}\left(\rho,{q}\right)=\frac{\Gamma\left(\rho\right).\Gamma\left({q}\right)}{\Gamma\left(\rho+{q}\right)}\:\Rightarrow \\ $$$$\mathrm{2}\rho−\mathrm{1}=\mathrm{0}\:{and}\:\mathrm{2}{q}−\mathrm{1}=\mathrm{1}+\frac{\mathrm{1}}{{n}} \\ $$$$\Rightarrow\rho=\frac{\mathrm{1}}{\mathrm{2}}\:{and}\:{q}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}} \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({sint}\right)^{\mathrm{1}+\frac{\mathrm{1}}{{n}}} {dt}=\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)}{\mathrm{2}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)} \\ $$$$=\frac{\sqrt{\pi}}{\mathrm{2}}×\frac{\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)}\:\Rightarrow \\ $$$${I}_{{n}} =\frac{{n}\pi}{\mathrm{2}\left({n}+\mathrm{1}\right)}−\frac{{n}}{{n}+\mathrm{1}}.\frac{\sqrt{\pi}}{\mathrm{2}}×\frac{\Gamma\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)}{\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}{n}}\right)} \\ $$
Commented by Mathspace last updated on 07/Jul/22
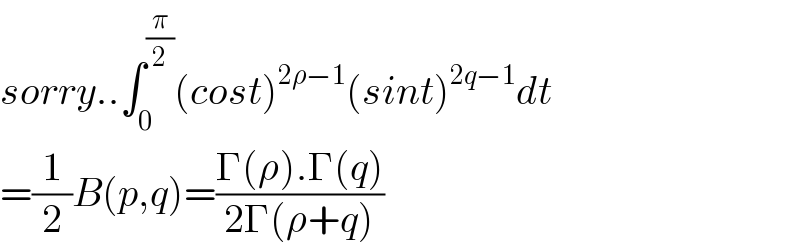
$${sorry}..\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \left({cost}\right)^{\mathrm{2}\rho−\mathrm{1}} \left({sint}\right)^{\mathrm{2}{q}−\mathrm{1}} {dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{B}\left({p},{q}\right)=\frac{\Gamma\left(\rho\right).\Gamma\left({q}\right)}{\mathrm{2}\Gamma\left(\rho+{q}\right)} \\ $$
Commented by Tawa11 last updated on 11/Jul/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
