Question Number 163487 by mnjuly1970 last updated on 07/Jan/22
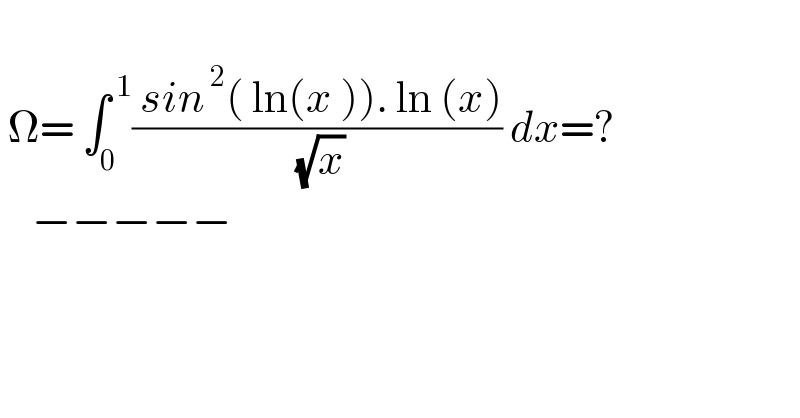
$$ \\ $$$$\:\Omega=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{sin}^{\:\mathrm{2}} \left(\:\mathrm{ln}\left({x}\:\right)\right).\:\mathrm{ln}\:\left({x}\right)}{\:\sqrt{{x}}}\:{dx}=? \\ $$$$\:\:\:\:−−−−− \\ $$
Answered by Lordose last updated on 07/Jan/22
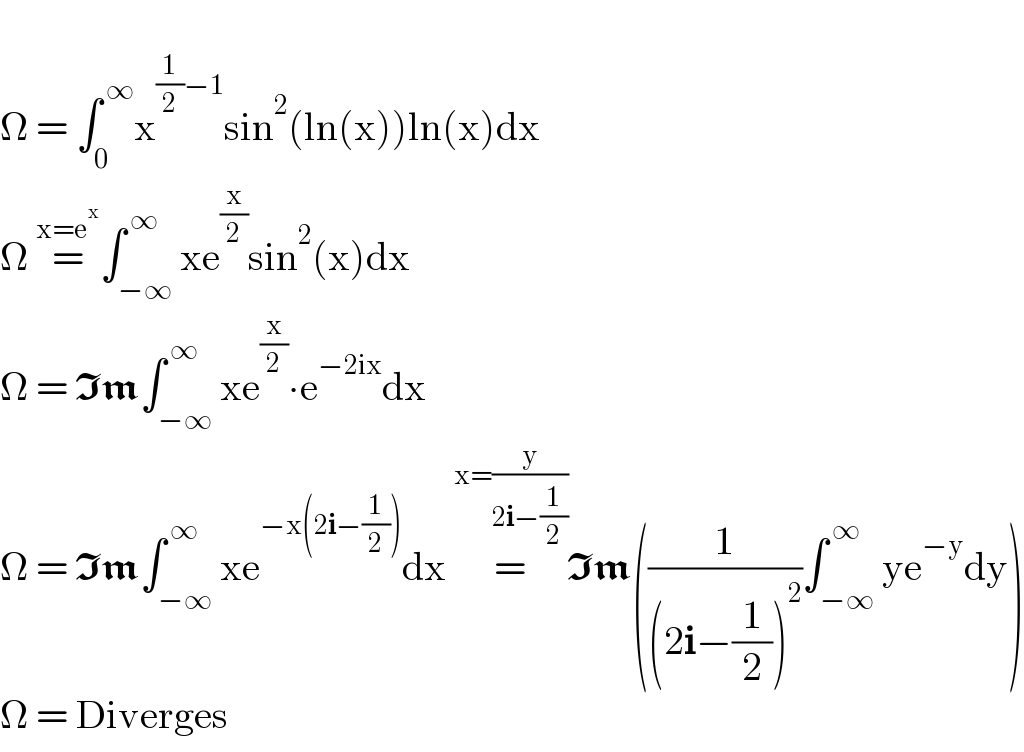
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{x}^{\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{ln}\left(\mathrm{x}\right)\right)\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{x}=\mathrm{e}^{\mathrm{x}} } {=}\int_{−\infty} ^{\:\infty} \mathrm{xe}^{\frac{\mathrm{x}}{\mathrm{2}}} \mathrm{sin}^{\mathrm{2}} \left(\mathrm{x}\right)\mathrm{dx} \\ $$$$\Omega\:=\:\boldsymbol{\mathfrak{Im}}\int_{−\infty} ^{\:\infty} \mathrm{xe}^{\frac{\mathrm{x}}{\mathrm{2}}} \centerdot\mathrm{e}^{−\mathrm{2ix}} \mathrm{dx} \\ $$$$\Omega\:=\:\boldsymbol{\mathfrak{Im}}\int_{−\infty} ^{\:\infty} \mathrm{xe}^{−\mathrm{x}\left(\mathrm{2}\boldsymbol{\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{2}}\right)} \mathrm{dx}\:\overset{\mathrm{x}=\frac{\mathrm{y}}{\mathrm{2}\boldsymbol{\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{2}}}} {=}\boldsymbol{\mathfrak{Im}}\left(\frac{\mathrm{1}}{\left(\mathrm{2}\boldsymbol{\mathrm{i}}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\int_{−\infty} ^{\:\infty} \mathrm{ye}^{−\mathrm{y}} \mathrm{dy}\right) \\ $$$$\Omega\:=\:\mathrm{Diverges} \\ $$
