Question Number 186193 by normans last updated on 02/Feb/23
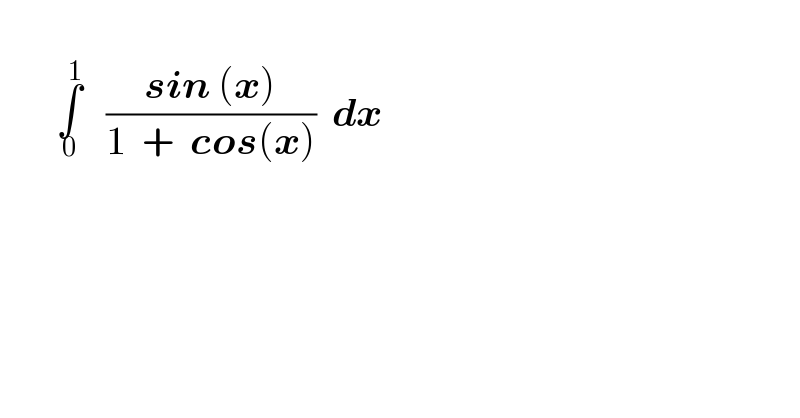
$$ \\ $$$$\:\:\:\:\:\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\:\:\frac{\boldsymbol{{sin}}\:\left(\boldsymbol{{x}}\right)}{\mathrm{1}\:\:+\:\:\boldsymbol{{cos}}\left(\boldsymbol{{x}}\right)}\:\:\boldsymbol{{dx}} \\ $$
Answered by CElcedricjunior last updated on 02/Feb/23
![∫_0 ^1 ((sinx)/(1+cosx))dx=−[ln(1+cosx)]_0 ^1 ∫_0 ^1 ((sinx)/(1+cosx))dx=ln2−ln(1+cos1) =======.=.==========..=. .............le celebre cedric junior...........](https://www.tinkutara.com/question/Q186227.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{sinx}}}{\mathrm{1}+\boldsymbol{{cosx}}}\boldsymbol{{dx}}=−\left[\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{cosx}}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{sinx}}}{\mathrm{1}+\boldsymbol{{cosx}}}\boldsymbol{{dx}}=\boldsymbol{{ln}}\mathrm{2}−\boldsymbol{{ln}}\left(\mathrm{1}+\boldsymbol{{cos}}\mathrm{1}\right) \\ $$$$=======.=.==========..=. \\ $$$$………….{le}\:{celebre}\:{cedric}\:{junior}……….. \\ $$$$ \\ $$
Answered by MJS_new last updated on 02/Feb/23
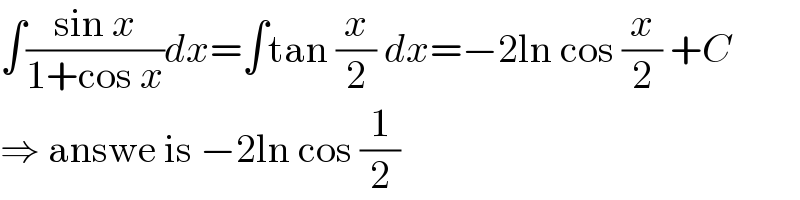
$$\int\frac{\mathrm{sin}\:{x}}{\mathrm{1}+\mathrm{cos}\:{x}}{dx}=\int\mathrm{tan}\:\frac{{x}}{\mathrm{2}}\:{dx}=−\mathrm{2ln}\:\mathrm{cos}\:\frac{{x}}{\mathrm{2}}\:+{C} \\ $$$$\Rightarrow\:\mathrm{answe}\:\mathrm{is}\:−\mathrm{2ln}\:\mathrm{cos}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
