0-1-sin-x-2cos-x-3sin-x-4cos-x-dx-

Question Number 41078 by Necxx last updated on 01/Aug/18

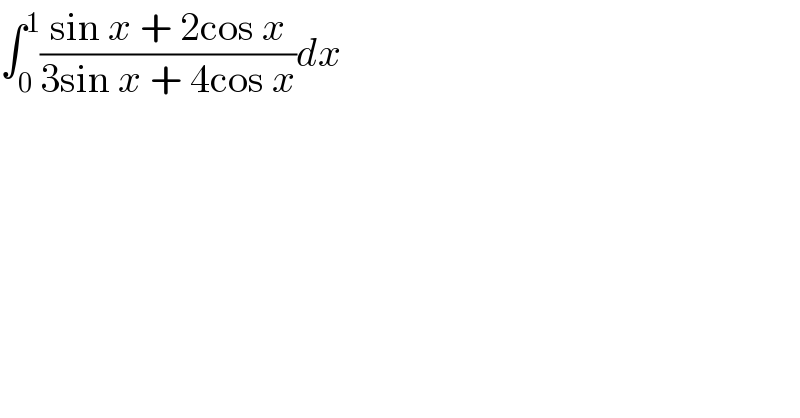
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{sin}\:{x}\:+\:\mathrm{2cos}\:{x}}{\mathrm{3sin}\:{x}\:+\:\mathrm{4cos}\:{x}}{dx} \\ $$

Commented by maxmathsup by imad last updated on 01/Aug/18

let I = ∫_0 ^1 ((sinx +2cosx)/(3sinx +4cosx))dx changement tan((x/2))=t give I = ∫_0 ^(tan((1/2))) ((((2t)/(1+t^2 )) + 2 ((1−t^2 )/(1+t^2 )))/(3((2t)/(1+t^2 )) +4((1−t^2 )/(1+t^2 )))) ((2dt)/(1+t^2 )) =2 ∫_0 ^(tan((1/2))) ((2t +2−2t^2 )/((1+t^2 )(6t +4−4t^2 ))) dt =−4 ∫_0 ^(tan((1/2))) ((t^2 −t−1)/(2(1+t^2 )(−2t^2 +3t +2)))dt =2 ∫_0 ^(tan((1/2))) ((t^2 −t−1)/((1+t^2 )(2t^2 −3t−2)))dt let decompose F(t)=((t^2 −t−1)/((t^2 +1)(2t^2 −3t−2))) roots of 2t^2 −3t −2 Δ =9 −4(2)(−2) =9 +16 =25 ⇒t_1 =((3+5)/4) =2 , t_2 =((3−5)/4) =−(1/2) F(t)=((t^2 −t−1)/((t−2)(t+(1/2))(t^2 +1))) =(a/(t−2)) +(b/(t+(1/2))) +((ct +d)/(t^2 +1)) a =lim_(t→2) (t−2)F(t)= (1/((5/2).5)) =(2/(25)) b =lim_(t→−(1/2)) (t+(1/2))F(t) =(((1/4)−(1/2)−1)/((−(1/2)−2)((5/4)))) =((−(5/4))/((−(5/2))((5/4)))) =(2/5) ⇒ F(t) = (2/(25(t−2))) +(2/(5(t+(1/2)))) +((ct+d)/(t^2 +1)) lim_(t→+∞) t F(t) =0=(2/(25)) +((10)/(25)) +c ⇒c=−((12)/(25)) F(t) =(2/(25(t−2) )) +(2/(5(t+(1/2)))) +((−((12)/(25))t +d)/(t^2 +1)) F(0) = ((−1)/((−1))) =1 = −(1/(25)) +(4/5) +d =((−1+20)/(25)) +d =((19)/(25)) +d ⇒d=1−((19)/(25)) d=(6/(25)) ⇒ F(t) = (2/(25(t−2))) +(2/(5(t+(1/2)))) +(1/(25)) ((−12t +6)/(t^2 +1)) ⇒ ∫ F(t)dt =(2/(25))ln∣t−2∣ +(2/5)ln∣t+(1/2)∣ −((12)/(25)) ∫ ((t−(1/2))/(t^2 +1))dt but ∫ ((t−(1/2))/(t^2 +1)) dt =(1/2) ∫ ((2t−1)/(t^2 +1)) dt =(1/2) ∫ ((2t+1−2)/(t^2 +1)) dt =(1/2)ln(t^2 +1) −arctan(t) ⇒ I = 2 ∫_0 ^(tan((1/2))) F(t)dt = 2[ (2/(25))ln∣t−2∣+(2/5)ln∣t+(1/2)∣−(6/(25))ln(t^2 +1) +((12)/(25))arctant]_0 ^(tan((1/2))) =(4/(25))ln∣tan((1/2))−2∣+(4/(25))ln∣tan((1/2))+(1/2)∣−((12)/(25))ln(tan^2 ((1/2))+1)+((24)/(50)) .

$${let}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{sinx}\:+\mathrm{2}{cosx}}{\mathrm{3}{sinx}\:+\mathrm{4}{cosx}}{dx}\:{changement}\:{tan}\left(\frac{{x}}{\mathrm{2}}\right)={t}\:{give} \\ $$$${I}\:=\:\int_{\mathrm{0}} ^{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:\:\:\frac{\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+\:\mathrm{2}\:\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}{\mathrm{3}\frac{\mathrm{2}{t}}{\mathrm{1}+{t}^{\mathrm{2}} }\:+\mathrm{4}\frac{\mathrm{1}−{t}^{\mathrm{2}} }{\mathrm{1}+{t}^{\mathrm{2}} }}\:\frac{\mathrm{2}{dt}}{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:\:\:\:\frac{\mathrm{2}{t}\:+\mathrm{2}−\mathrm{2}{t}^{\mathrm{2}} }{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{6}{t}\:+\mathrm{4}−\mathrm{4}{t}^{\mathrm{2}} \right)}\:{dt}\:\:=−\mathrm{4}\:\int_{\mathrm{0}} ^{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:\:\frac{{t}^{\mathrm{2}} −{t}−\mathrm{1}}{\mathrm{2}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(−\mathrm{2}{t}^{\mathrm{2}} \:+\mathrm{3}{t}\:+\mathrm{2}\right)}{dt} \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \:\frac{{t}^{\mathrm{2}} −{t}−\mathrm{1}}{\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\mathrm{2}{t}^{\mathrm{2}} \:−\mathrm{3}{t}−\mathrm{2}\right)}{dt}\:{let}\:{decompose}\:{F}\left({t}\right)=\frac{{t}^{\mathrm{2}} −{t}−\mathrm{1}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)\left(\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}−\mathrm{2}\right)} \\ $$$${roots}\:{of}\:\mathrm{2}{t}^{\mathrm{2}} −\mathrm{3}{t}\:−\mathrm{2} \\ $$$$\Delta\:=\mathrm{9}\:−\mathrm{4}\left(\mathrm{2}\right)\left(−\mathrm{2}\right)\:=\mathrm{9}\:+\mathrm{16}\:=\mathrm{25}\:\Rightarrow{t}_{\mathrm{1}} =\frac{\mathrm{3}+\mathrm{5}}{\mathrm{4}}\:=\mathrm{2}\:\:,\:\:{t}_{\mathrm{2}} =\frac{\mathrm{3}−\mathrm{5}}{\mathrm{4}}\:=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${F}\left({t}\right)=\frac{{t}^{\mathrm{2}} −{t}−\mathrm{1}}{\left({t}−\mathrm{2}\right)\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)}\:=\frac{{a}}{{t}−\mathrm{2}}\:+\frac{{b}}{{t}+\frac{\mathrm{1}}{\mathrm{2}}}\:+\frac{{ct}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${a}\:={lim}_{{t}\rightarrow\mathrm{2}} \left({t}−\mathrm{2}\right){F}\left({t}\right)=\:\frac{\mathrm{1}}{\frac{\mathrm{5}}{\mathrm{2}}.\mathrm{5}}\:=\frac{\mathrm{2}}{\mathrm{25}} \\ $$$${b}\:={lim}_{{t}\rightarrow−\frac{\mathrm{1}}{\mathrm{2}}} \:\:\:\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right){F}\left({t}\right)\:=\frac{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{1}}{\left(−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}\right)\left(\frac{\mathrm{5}}{\mathrm{4}}\right)}\:=\frac{−\frac{\mathrm{5}}{\mathrm{4}}}{\left(−\frac{\mathrm{5}}{\mathrm{2}}\right)\left(\frac{\mathrm{5}}{\mathrm{4}}\right)}\:=\frac{\mathrm{2}}{\mathrm{5}}\:\Rightarrow \\ $$$${F}\left({t}\right)\:=\:\frac{\mathrm{2}}{\mathrm{25}\left({t}−\mathrm{2}\right)}\:+\frac{\mathrm{2}}{\mathrm{5}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:+\frac{{ct}+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${lim}_{{t}\rightarrow+\infty} {t}\:{F}\left({t}\right)\:=\mathrm{0}=\frac{\mathrm{2}}{\mathrm{25}}\:+\frac{\mathrm{10}}{\mathrm{25}}\:+{c}\:\Rightarrow{c}=−\frac{\mathrm{12}}{\mathrm{25}} \\ $$$${F}\left({t}\right)\:=\frac{\mathrm{2}}{\mathrm{25}\left({t}−\mathrm{2}\right)\:}\:+\frac{\mathrm{2}}{\mathrm{5}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:+\frac{−\frac{\mathrm{12}}{\mathrm{25}}{t}\:+{d}}{{t}^{\mathrm{2}} \:+\mathrm{1}} \\ $$$${F}\left(\mathrm{0}\right)\:=\:\frac{−\mathrm{1}}{\left(−\mathrm{1}\right)}\:=\mathrm{1}\:=\:−\frac{\mathrm{1}}{\mathrm{25}}\:+\frac{\mathrm{4}}{\mathrm{5}}\:+{d}\:=\frac{−\mathrm{1}+\mathrm{20}}{\mathrm{25}}\:+{d}\:=\frac{\mathrm{19}}{\mathrm{25}}\:+{d}\:\Rightarrow{d}=\mathrm{1}−\frac{\mathrm{19}}{\mathrm{25}} \\ $$$${d}=\frac{\mathrm{6}}{\mathrm{25}}\:\Rightarrow\:{F}\left({t}\right)\:=\:\frac{\mathrm{2}}{\mathrm{25}\left({t}−\mathrm{2}\right)}\:+\frac{\mathrm{2}}{\mathrm{5}\left({t}+\frac{\mathrm{1}}{\mathrm{2}}\right)}\:+\frac{\mathrm{1}}{\mathrm{25}}\:\frac{−\mathrm{12}{t}\:+\mathrm{6}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:\Rightarrow \\ $$$$\int\:{F}\left({t}\right){dt}\:=\frac{\mathrm{2}}{\mathrm{25}}{ln}\mid{t}−\mathrm{2}\mid\:\:+\frac{\mathrm{2}}{\mathrm{5}}{ln}\mid{t}+\frac{\mathrm{1}}{\mathrm{2}}\mid\:−\frac{\mathrm{12}}{\mathrm{25}}\:\int\:\:\frac{{t}−\frac{\mathrm{1}}{\mathrm{2}}}{{t}^{\mathrm{2}} \:+\mathrm{1}}{dt}\:{but} \\ $$$$\int\:\:\:\frac{{t}−\frac{\mathrm{1}}{\mathrm{2}}}{{t}^{\mathrm{2}} +\mathrm{1}}\:{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\:\frac{\mathrm{2}{t}−\mathrm{1}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\:\int\:\frac{\mathrm{2}{t}+\mathrm{1}−\mathrm{2}}{{t}^{\mathrm{2}} \:+\mathrm{1}}\:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\:−{arctan}\left({t}\right)\:\Rightarrow \\ $$$${I}\:=\:\mathrm{2}\:\int_{\mathrm{0}} ^{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} {F}\left({t}\right){dt}\:=\:\mathrm{2}\left[\:\frac{\mathrm{2}}{\mathrm{25}}{ln}\mid{t}−\mathrm{2}\mid+\frac{\mathrm{2}}{\mathrm{5}}{ln}\mid{t}+\frac{\mathrm{1}}{\mathrm{2}}\mid−\frac{\mathrm{6}}{\mathrm{25}}{ln}\left({t}^{\mathrm{2}} \:+\mathrm{1}\right)\:+\frac{\mathrm{12}}{\mathrm{25}}{arctant}\right]_{\mathrm{0}} ^{{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)} \\ $$$$=\frac{\mathrm{4}}{\mathrm{25}}{ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)−\mathrm{2}\mid+\frac{\mathrm{4}}{\mathrm{25}}{ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\frac{\mathrm{1}}{\mathrm{2}}\mid−\frac{\mathrm{12}}{\mathrm{25}}{ln}\left({tan}^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)+\mathrm{1}\right)+\frac{\mathrm{24}}{\mathrm{50}}\:. \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Commented by Necxx last updated on 02/Aug/18

$${thank}\:{you}\:{so}\:{much}\:{sir} \\ $$

Commented by turbo msup by abdo last updated on 02/Aug/18

$${you}\:{re}\:{welcome}\:{sir} \\ $$

Answered by tanmay.chaudhury50@gmail.com last updated on 01/Aug/18

sinx+2cosx=a(3sinx+4cosx)+b.(d/dx)(3sinx+4cosx) ∫((a(3sinx+4cosx)+b(d/dx)(3sinx+4cisx))/(3sinx+4cosx)) dx ∫adx+b∫(((d/dx)(3sinx+4cosx))/(3sinx+4cosx))dx a∫dx+b∫((d(3sinx+4cosx))/(3sinx+4cosx)) ax+bln(3sinx+4cosx)+c now finding the value of a and b sinx+2cosx=a(3sinx+4cosx)+b(3cosx−4sinx) sinx+2cosx=(3a−4b)sinx+(4a+3b)cosx 3a−4b=1......×3 4a+3b=2 .....×4 9a−12b=3 16a+12b=8 25b=11 b=((11)/(25)) 3a=1+4b 3a=1+((44)/(25)) 3a=((69)/(25)) a=((23)/(25)) so the answer is ((23)/(25))x+((11)/(25))ln(3sinx+4cosx)+c

$${sinx}+\mathrm{2}{cosx}={a}\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right)+{b}.\frac{{d}}{{dx}}\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right) \\ $$$$\int\frac{{a}\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right)+{b}\frac{{d}}{{dx}}\left(\mathrm{3}{sinx}+\mathrm{4}{cisx}\right)}{\mathrm{3}{sinx}+\mathrm{4}{cosx}}\:{dx} \\ $$$$\int{adx}+{b}\int\frac{\frac{{d}}{{dx}}\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right)}{\mathrm{3}{sinx}+\mathrm{4}{cosx}}{dx} \\ $$$${a}\int{dx}+{b}\int\frac{{d}\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right)}{\mathrm{3}{sinx}+\mathrm{4}{cosx}} \\ $$$${ax}+{bln}\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right)+{c} \\ $$$${now}\:{finding}\:{the}\:{value}\:{of}\:{a}\:\:{and}\:{b} \\ $$$${sinx}+\mathrm{2}{cosx}={a}\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right)+{b}\left(\mathrm{3}{cosx}−\mathrm{4}{sinx}\right) \\ $$$${sinx}+\mathrm{2}{cosx}=\left(\mathrm{3}{a}−\mathrm{4}{b}\right){sinx}+\left(\mathrm{4}{a}+\mathrm{3}{b}\right){cosx} \\ $$$$\mathrm{3}{a}−\mathrm{4}{b}=\mathrm{1}……×\mathrm{3} \\ $$$$\mathrm{4}{a}+\mathrm{3}{b}=\mathrm{2}\:…..×\mathrm{4} \\ $$$$\mathrm{9}{a}−\mathrm{12}{b}=\mathrm{3} \\ $$$$\mathrm{16}{a}+\mathrm{12}{b}=\mathrm{8} \\ $$$$\mathrm{25}{b}=\mathrm{11}\:\:{b}=\frac{\mathrm{11}}{\mathrm{25}} \\ $$$$\mathrm{3}{a}=\mathrm{1}+\mathrm{4}{b} \\ $$$$\mathrm{3}{a}=\mathrm{1}+\frac{\mathrm{44}}{\mathrm{25}} \\ $$$$\mathrm{3}{a}=\frac{\mathrm{69}}{\mathrm{25}}\:\:\:\:{a}=\frac{\mathrm{23}}{\mathrm{25}} \\ $$$${so}\:{the}\:{answer}\:{is}\: \\ $$$$\frac{\mathrm{23}}{\mathrm{25}}{x}+\frac{\mathrm{11}}{\mathrm{25}}{ln}\left(\mathrm{3}{sinx}+\mathrm{4}{cosx}\right)+{c} \\ $$

Commented by Necxx last updated on 02/Aug/18