Question Number 177906 by cortano1 last updated on 11/Oct/22
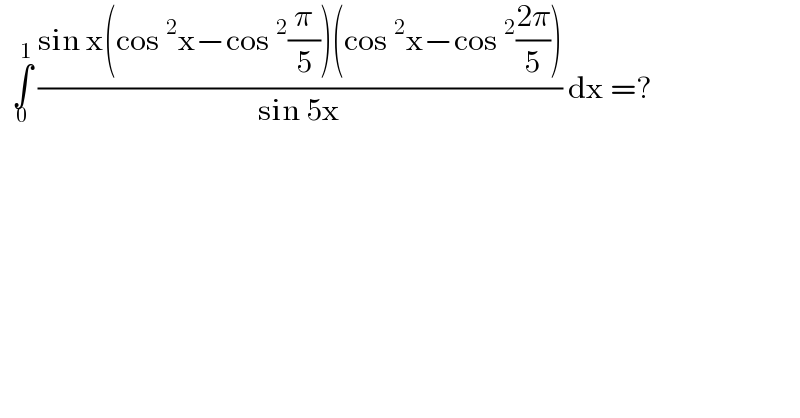
$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{sin}\:\mathrm{x}\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cos}\:^{\mathrm{2}} \frac{\pi}{\mathrm{5}}\right)\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cos}\:^{\mathrm{2}} \frac{\mathrm{2}\pi}{\mathrm{5}}\right)}{\mathrm{sin}\:\mathrm{5x}}\:\mathrm{dx}\:=? \\ $$
Answered by Frix last updated on 11/Oct/22
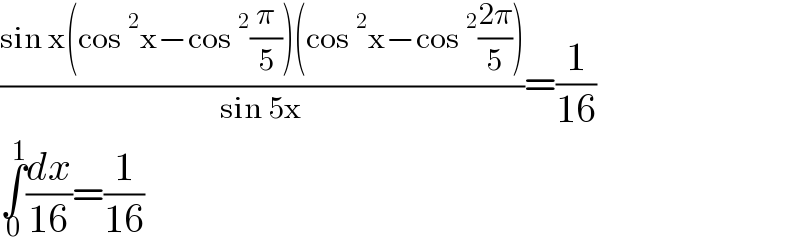
$$\frac{\mathrm{sin}\:\mathrm{x}\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cos}\:^{\mathrm{2}} \frac{\pi}{\mathrm{5}}\right)\left(\mathrm{cos}\:^{\mathrm{2}} \mathrm{x}−\mathrm{cos}\:^{\mathrm{2}} \frac{\mathrm{2}\pi}{\mathrm{5}}\right)}{\mathrm{sin}\:\mathrm{5x}}=\frac{\mathrm{1}}{\mathrm{16}} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{dx}}{\mathrm{16}}=\frac{\mathrm{1}}{\mathrm{16}} \\ $$
Commented by Frix last updated on 11/Oct/22

$$\mathrm{sin}\:{x}\:={s} \\ $$$$\Rightarrow \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:−\mathrm{cos}^{\mathrm{2}} \:\frac{\pi}{\mathrm{5}}\:=−{s}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{8}}−\frac{\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$\mathrm{cos}^{\mathrm{2}} \:{x}\:−\mathrm{cos}^{\mathrm{2}} \:\frac{\mathrm{2}\pi}{\mathrm{5}}\:=−{s}^{\mathrm{2}} +\frac{\mathrm{5}}{\mathrm{8}}+\frac{\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$\mathrm{sin}\:\mathrm{5}{x}\:=\mathrm{16}{s}^{\mathrm{5}} −\mathrm{20}{s}^{\mathrm{3}} +\mathrm{5}{s} \\ $$$$\mathrm{the}\:\mathrm{rest}\:\mathrm{is}\:\mathrm{easy} \\ $$
