Question Number 155930 by talminator2856791 last updated on 06/Oct/21
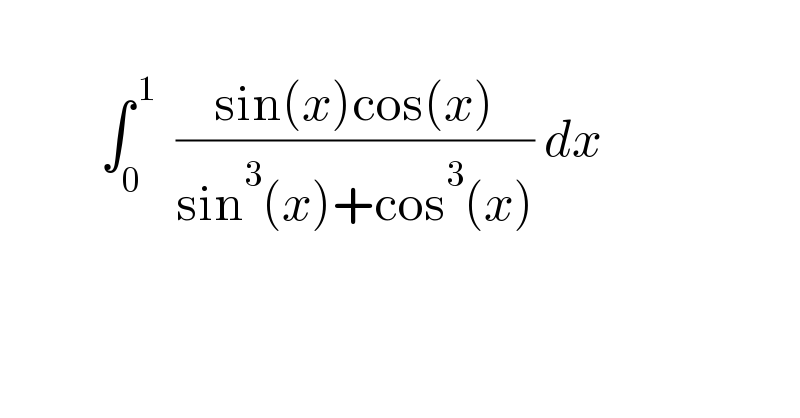
$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\:\frac{\mathrm{sin}\left({x}\right)\mathrm{cos}\left({x}\right)}{\mathrm{sin}^{\mathrm{3}} \left({x}\right)+\mathrm{cos}^{\mathrm{3}} \left({x}\right)}\:{dx} \\ $$$$\: \\ $$
Commented by talminator2856791 last updated on 06/Oct/21
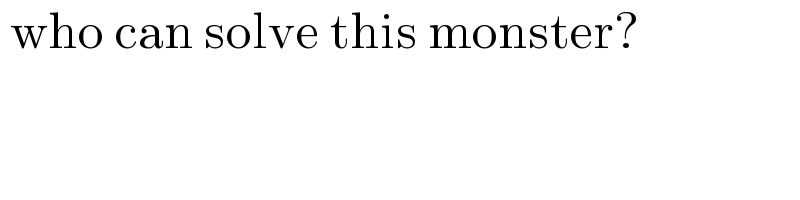
$$\:\mathrm{who}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{monster}? \\ $$
Commented by MJS_new last updated on 06/Oct/21
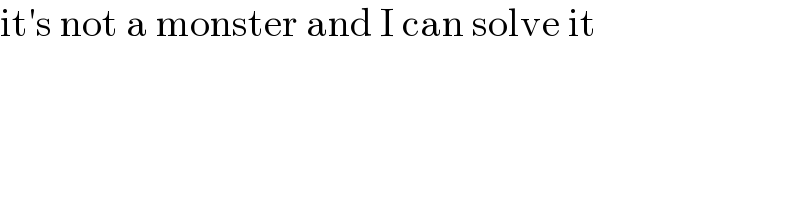
$$\mathrm{it}'\mathrm{s}\:\mathrm{not}\:\mathrm{a}\:\mathrm{monster}\:\mathrm{and}\:\mathrm{I}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{it} \\ $$
Answered by MJS_new last updated on 06/Oct/21
![∫((sin x cos x)/(sin^3 x +cos^3 x))dx= =(1/3)∫((sin x +cos x)/(1−sin x cos x))dx−(1/3)∫(dx/(sin x +cos x)) (1/3)∫((sin x +cos x)/(1−sin x cos x))dx= [t=cos (x+(π/4)) → dx=−(dt/(sin (x+(π/4))))] =−((2(√2))/3)∫(dt/(2t^2 +1))=−(2/3)arctan (√2)t =... =(2/3)arctan (sin x −cos x) (1/3)∫(dx/(sin x +cos x))= [t=tan ((x/2)+(π/8)) → dx=((2dt)/(t^2 +1))] =((√2)/6)∫(dt/t)=((√2)/6)ln t =((√2)/6)ln tan ((x/2)+(π/8)) = =((√2)/6)ln (((√2)+2sin x)/( (√2)+2cos x)) ∫((sin x cos x)/(sin^3 x +cos^3 x))dx= =(2/3)arctan (sin x −cos x) −((√2)/6)ln (((√2)+2sin x)/( (√2)+2cos x)) +C](https://www.tinkutara.com/question/Q155944.png)
$$\int\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{cos}^{\mathrm{3}} \:{x}}{dx}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{dx}−\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}} \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}{\mathrm{1}−\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{cos}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)\:\rightarrow\:{dx}=−\frac{{dt}}{\mathrm{sin}\:\left({x}+\frac{\pi}{\mathrm{4}}\right)}\right] \\ $$$$=−\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}\int\frac{{dt}}{\mathrm{2}{t}^{\mathrm{2}} +\mathrm{1}}=−\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\sqrt{\mathrm{2}}{t}\:=… \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\right) \\ $$$$ \\ $$$$\frac{\mathrm{1}}{\mathrm{3}}\int\frac{{dx}}{\mathrm{sin}\:{x}\:+\mathrm{cos}\:{x}}= \\ $$$$\:\:\:\:\:\left[{t}=\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)\:\rightarrow\:{dx}=\frac{\mathrm{2}{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}\right] \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\int\frac{{dt}}{{t}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\mathrm{ln}\:{t}\:=\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\mathrm{ln}\:\mathrm{tan}\:\left(\frac{{x}}{\mathrm{2}}+\frac{\pi}{\mathrm{8}}\right)\:= \\ $$$$=\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}+\mathrm{2sin}\:{x}}{\:\sqrt{\mathrm{2}}+\mathrm{2cos}\:{x}} \\ $$$$ \\ $$$$\int\frac{\mathrm{sin}\:{x}\:\mathrm{cos}\:{x}}{\mathrm{sin}^{\mathrm{3}} \:{x}\:+\mathrm{cos}^{\mathrm{3}} \:{x}}{dx}= \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\mathrm{arctan}\:\left(\mathrm{sin}\:{x}\:−\mathrm{cos}\:{x}\right)\:−\frac{\sqrt{\mathrm{2}}}{\mathrm{6}}\mathrm{ln}\:\frac{\sqrt{\mathrm{2}}+\mathrm{2sin}\:{x}}{\:\sqrt{\mathrm{2}}+\mathrm{2cos}\:{x}}\:+{C} \\ $$
Commented by Tawa11 last updated on 06/Oct/21

$$\mathrm{Great}\:\mathrm{sir} \\ $$
