Question Number 187453 by norboyev last updated on 17/Feb/23
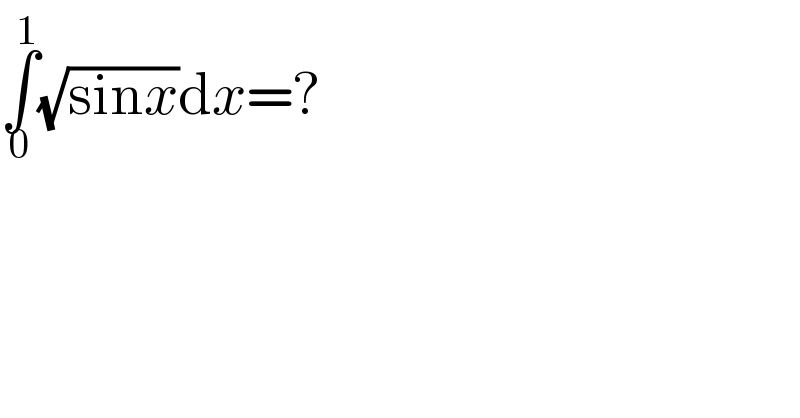
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{sin}{x}}\mathrm{d}{x}=? \\ $$
Answered by Frix last updated on 17/Feb/23
![∫(√(sin x)) dx= [Elliptic Integral] =−2E ((π/4)−(x/2)∣2) +C ∫_0 ^1 (√(sin x)) dx≈.642977634658](https://www.tinkutara.com/question/Q187454.png)
$$\int\sqrt{\mathrm{sin}\:{x}}\:{dx}=\:\left[\mathrm{Elliptic}\:\mathrm{Integral}\right] \\ $$$$=−\mathrm{2}{E}\:\left(\frac{\pi}{\mathrm{4}}−\frac{{x}}{\mathrm{2}}\mid\mathrm{2}\right)\:+{C} \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{sin}\:{x}}\:{dx}\approx.\mathrm{642977634658} \\ $$
Answered by CElcedricjunior last updated on 21/Feb/23
![∫_0 ^1 (√(sinx))dx=k posons sinx=t^2 =>dx=((2t)/( (√(1−t^2 ))))dt qd: { ((x−>0 )),((x−>1)) :}=> { ((t−>0)),((t−>sin(1))) :} k=∫_0 ^(sin(1)) ((2t^3 )/( (√(1−t^2 ))))dt { ((u=t^2 )),((v′=(t/( (√(1−t^2 )))))) :}=> { ((u′=2t)),((v=−(√(1−t^2 )))) :}★Moivre k=−2sin^2 (1)∣cos(1)∣+4∫_0 ^(sin(1)) t(√(1−t^2 ))dt k=−sin(1)sin(2)+4[−(2/3)(√((1−t^2 )))]_0 ^(sin(1)) ■Cedric junior k=sin(1)sin(2)−(8/3)cos^(3/2) (1)+(8/3)](https://www.tinkutara.com/question/Q187742.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\boldsymbol{{sinx}}}\boldsymbol{{dx}}=\boldsymbol{{k}} \\ $$$$\boldsymbol{{posons}}\:\boldsymbol{{sinx}}=\boldsymbol{{t}}^{\mathrm{2}} =>\boldsymbol{{dx}}=\frac{\mathrm{2}\boldsymbol{{t}}}{\:\sqrt{\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} }}\boldsymbol{{dt}} \\ $$$$\boldsymbol{{qd}}:\begin{cases}{\boldsymbol{{x}}−>\mathrm{0}\:}\\{\boldsymbol{{x}}−>\mathrm{1}}\end{cases}=>\begin{cases}{\boldsymbol{{t}}−>\mathrm{0}}\\{\boldsymbol{{t}}−>\boldsymbol{{sin}}\left(\mathrm{1}\right)}\end{cases} \\ $$$$\boldsymbol{{k}}=\int_{\mathrm{0}} ^{\boldsymbol{{sin}}\left(\mathrm{1}\right)} \frac{\mathrm{2}\boldsymbol{{t}}^{\mathrm{3}} }{\:\sqrt{\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} }}\boldsymbol{{dt}} \\ $$$$\begin{cases}{\boldsymbol{{u}}=\boldsymbol{{t}}^{\mathrm{2}} }\\{\boldsymbol{{v}}'=\frac{\boldsymbol{{t}}}{\:\sqrt{\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} }}}\end{cases}=>\begin{cases}{\boldsymbol{{u}}'=\mathrm{2}\boldsymbol{{t}}}\\{\boldsymbol{{v}}=−\sqrt{\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} }}\end{cases}\bigstar{Moivre} \\ $$$$\boldsymbol{{k}}=−\mathrm{2}\boldsymbol{{si}}\overset{\mathrm{2}} {\boldsymbol{{n}}}\left(\mathrm{1}\right)\mid\boldsymbol{{cos}}\left(\mathrm{1}\right)\mid+\mathrm{4}\int_{\mathrm{0}} ^{\boldsymbol{{sin}}\left(\mathrm{1}\right)} \boldsymbol{{t}}\sqrt{\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} }\boldsymbol{{dt}} \\ $$$$\boldsymbol{{k}}=−\boldsymbol{{sin}}\left(\mathrm{1}\right)\boldsymbol{{sin}}\left(\mathrm{2}\right)+\mathrm{4}\left[−\frac{\mathrm{2}}{\mathrm{3}}\sqrt{\left(\mathrm{1}−\boldsymbol{{t}}^{\mathrm{2}} \right)}\right]_{\mathrm{0}} ^{\boldsymbol{{sin}}\left(\mathrm{1}\right)} \:\blacksquare\mathscr{C}{edric}\:{junior} \\ $$$$\boldsymbol{{k}}=\boldsymbol{{sin}}\left(\mathrm{1}\right)\boldsymbol{{sin}}\left(\mathrm{2}\right)−\frac{\mathrm{8}}{\mathrm{3}}\boldsymbol{{co}}\overset{\frac{\mathrm{3}}{\mathrm{2}}} {\boldsymbol{{s}}}\left(\mathrm{1}\right)+\frac{\mathrm{8}}{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
