Question Number 146752 by Bens last updated on 15/Jul/21
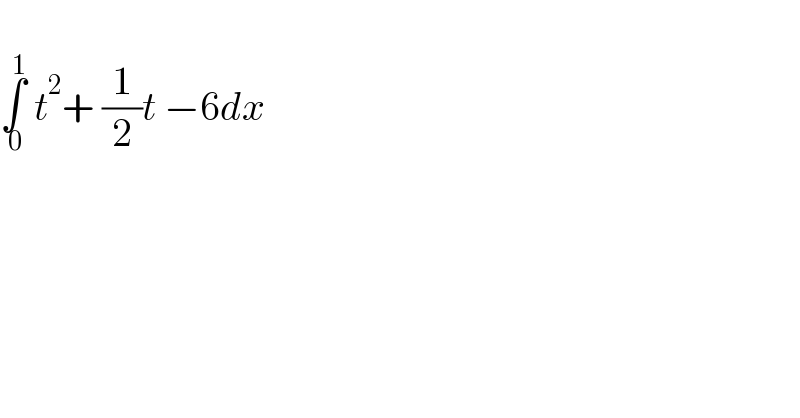
$$ \\ $$$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:{t}^{\mathrm{2}} +\:\frac{\mathrm{1}}{\mathrm{2}}{t}\:−\mathrm{6}{dx}\:\: \\ $$
Answered by puissant last updated on 15/Jul/21
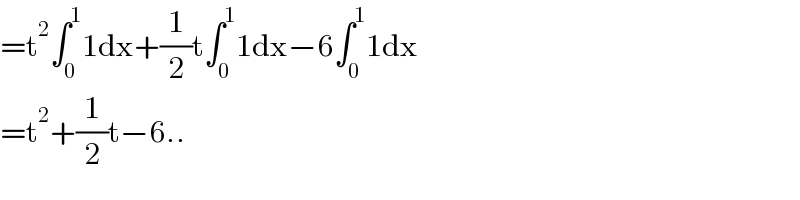
$$=\mathrm{t}^{\mathrm{2}} \int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1dx}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1dx}−\mathrm{6}\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{1dx} \\ $$$$=\mathrm{t}^{\mathrm{2}} +\frac{\mathrm{1}}{\mathrm{2}}\mathrm{t}−\mathrm{6}.. \\ $$
