Question Number 146756 by Bens last updated on 15/Jul/21

$$ \\ $$$$ \\ $$$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:{t}^{\mathrm{2}} \:+\:\mathrm{1}\:{dt} \\ $$
Answered by tabata last updated on 15/Jul/21
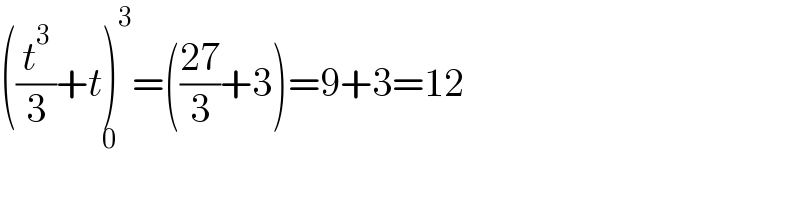
$$\left(\frac{{t}^{\mathrm{3}} }{\mathrm{3}}+{t}\underset{\mathrm{0}} {\right)}^{\mathrm{3}} =\left(\frac{\mathrm{27}}{\mathrm{3}}+\mathrm{3}\right)=\mathrm{9}+\mathrm{3}=\mathrm{12} \\ $$
Answered by puissant last updated on 15/Jul/21
![=[(t^3 /3)+t]_0 ^1 = (4/3)..](https://www.tinkutara.com/question/Q146763.png)
$$=\left[\frac{\mathrm{t}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{t}\right]_{\mathrm{0}} ^{\mathrm{1}} =\:\frac{\mathrm{4}}{\mathrm{3}}.. \\ $$
