Question Number 35379 by lilesh7 last updated on 18/May/18
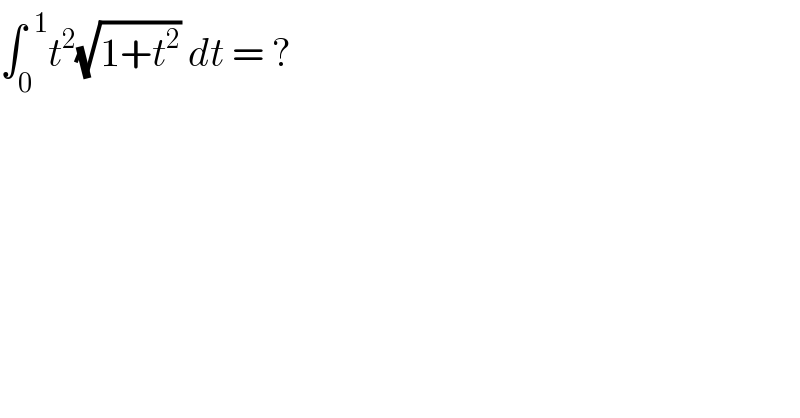
$$\int_{\mathrm{0}} ^{\:\:\mathrm{1}} {t}^{\mathrm{2}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}\:=\:? \\ $$
Commented by prof Abdo imad last updated on 18/May/18
![let put I = ∫_0 ^1 t^2 (√(1+t^2 )) dt.changement t=shx give I = ∫_0 ^(ln(1+(√(2)))) sh^2 x chx.chxdx =∫_0 ^(ln(1+(√2))) (shx chx)^2 dx =(1/4) ∫_0 ^(ln(1+(√2))) sh^2 (2x)dx =(1/4) ∫_0 ^(ln(1+(√2))) ((ch(4x)−1)/2)dx =(1/8) ∫_0 ^(ln(1+(√2))) ch(4x)dx −(1/8)ln(1+(√2)) = (1/(32))[ sh(4x)]_0 ^(ln(1+(√2))) −(1/8)ln(1+(√2)) =(1/(32)) sh(4ln(1+(√(2)))) −(1/8)ln(1+(√2)) but we have shx =((e^x −e^(−x) )/2) ⇒sh(4ln(1+(√(2)))) =((e^(4ln(1+(√2))) − e^(−4ln(1+(√2))) )/2)=(((1+(√2))^4 −(1/((1+(√2))^4 )))/2)⇒ I = (1/(64)){ (1+(√2))^4 −(1+(√2))^(−4) } −(1/8)ln(1+(√2)) let remember that argsh(x)=ln(x+(√(x^2 +1))) argchx=ln(x +(√(x^2 −1)))](https://www.tinkutara.com/question/Q35398.png)
$${let}\:{put}\:{I}\:=\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{t}^{\mathrm{2}} \:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\:{dt}.{changement}\:{t}={shx} \\ $$$${give}\:{I}\:=\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\left.\mathrm{2}\right)}\right.} \:\:{sh}^{\mathrm{2}} {x}\:{chx}.{chxdx} \\ $$$$=\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:\left({shx}\:{chx}\right)^{\mathrm{2}} {dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} {sh}^{\mathrm{2}} \left(\mathrm{2}{x}\right){dx}\:=\frac{\mathrm{1}}{\mathrm{4}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\frac{{ch}\left(\mathrm{4}{x}\right)−\mathrm{1}}{\mathrm{2}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}}\:\int_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} {ch}\left(\mathrm{4}{x}\right){dx}\:−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{32}}\left[\:{sh}\left(\mathrm{4}{x}\right)\right]_{\mathrm{0}} ^{{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:\:−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{32}}\:{sh}\left(\mathrm{4}{ln}\left(\mathrm{1}+\sqrt{\left.\mathrm{2}\right)}\right)\:−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)\:{but}\:{we}\:{have}\right. \\ $$$${shx}\:=\frac{{e}^{{x}} \:\:−{e}^{−{x}} }{\mathrm{2}}\:\Rightarrow{sh}\left(\mathrm{4}{ln}\left(\mathrm{1}+\sqrt{\left.\mathrm{2}\left.\right)\right)}\right.\right. \\ $$$$=\frac{{e}^{\mathrm{4}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} \:−\:{e}^{−\mathrm{4}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)} }{\mathrm{2}}=\frac{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \:\:−\frac{\mathrm{1}}{\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} }}{\mathrm{2}}\Rightarrow \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{64}}\left\{\:\:\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{\mathrm{4}} \:−\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)^{−\mathrm{4}} \right\}\:−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$$${let}\:{remember}\:{that} \\ $$$${argsh}\left({x}\right)={ln}\left({x}+\sqrt{\left.{x}^{\mathrm{2}} +\mathrm{1}\right)}\right. \\ $$$${argchx}={ln}\left({x}\:+\sqrt{{x}^{\mathrm{2}} −\mathrm{1}}\right) \\ $$$$ \\ $$
Commented by ajfour last updated on 18/May/18
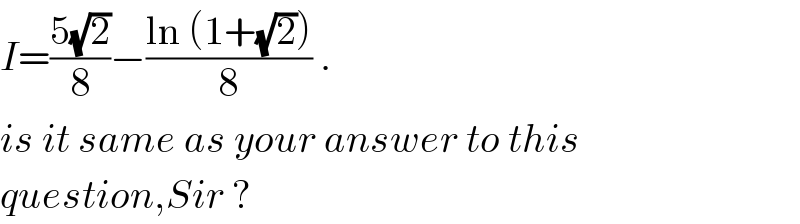
$${I}=\frac{\mathrm{5}\sqrt{\mathrm{2}}}{\mathrm{8}}−\frac{\mathrm{ln}\:\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)}{\mathrm{8}}\:. \\ $$$${is}\:{it}\:{same}\:{as}\:{your}\:{answer}\:{to}\:{this} \\ $$$${question},{Sir}\:? \\ $$
Commented by abdo mathsup 649 cc last updated on 18/May/18
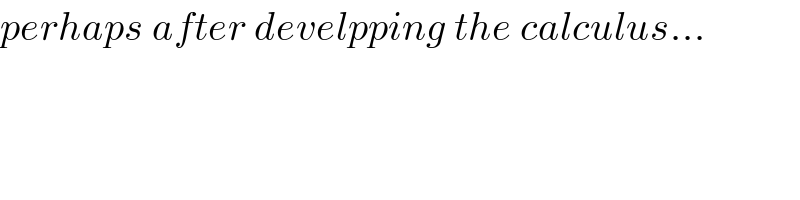
$${perhaps}\:{after}\:{develpping}\:{the}\:{calculus}… \\ $$
Answered by MJS last updated on 18/May/18
![∫t^2 (√(t^2 +1))dt=∫(t^2 +1−1)(√(t^2 +1))dt= =∫((t^2 +1)(√(t^2 +1))−(√(t^2 +1)))dt= =∫(t^2 +1)^(3/2) dt−∫(t^2 +1)^(1/2) dt= [t=tan(u) → dt=sec^2 (u)du] =∫sec^2 (u)(tan^2 (u)+1)^(3/2) du−∫sec^2 (u)(tan^2 (u)+1)^(1/2) du= [tan^2 (u)+1=sec^2 (u)] =∫sec^5 (u)du−∫sec^3 (u)du now use the reduction formula ∫sec^n (α)dα=((sec^(n−2) (α)tan(α))/(n−1))+((n−2)/(n−1))∫sec^(n−2) (α)dα](https://www.tinkutara.com/question/Q35386.png)
$$\int{t}^{\mathrm{2}} \sqrt{{t}^{\mathrm{2}} +\mathrm{1}}{dt}=\int\left({t}^{\mathrm{2}} +\mathrm{1}−\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}{dt}= \\ $$$$=\int\left(\left({t}^{\mathrm{2}} +\mathrm{1}\right)\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}−\sqrt{{t}^{\mathrm{2}} +\mathrm{1}}\right){dt}= \\ $$$$=\int\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {dt}−\int\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dt}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[{t}=\mathrm{tan}\left({u}\right)\:\rightarrow\:{dt}=\mathrm{sec}^{\mathrm{2}} \left({u}\right){du}\right] \\ $$$$=\int\mathrm{sec}^{\mathrm{2}} \left({u}\right)\left(\mathrm{tan}^{\mathrm{2}} \left({u}\right)+\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {du}−\int\mathrm{sec}^{\mathrm{2}} \left({u}\right)\left(\mathrm{tan}^{\mathrm{2}} \left({u}\right)+\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {du}= \\ $$$$\:\:\:\:\:\:\:\:\:\:\left[\mathrm{tan}^{\mathrm{2}} \left({u}\right)+\mathrm{1}=\mathrm{sec}^{\mathrm{2}} \left({u}\right)\right] \\ $$$$=\int\mathrm{sec}^{\mathrm{5}} \left({u}\right){du}−\int\mathrm{sec}^{\mathrm{3}} \left({u}\right){du} \\ $$$$ \\ $$$$\mathrm{now}\:\mathrm{use}\:\mathrm{the}\:\mathrm{reduction}\:\mathrm{formula} \\ $$$$\int\mathrm{sec}^{{n}} \left(\alpha\right){d}\alpha=\frac{\mathrm{sec}^{{n}−\mathrm{2}} \left(\alpha\right)\mathrm{tan}\left(\alpha\right)}{{n}−\mathrm{1}}+\frac{{n}−\mathrm{2}}{{n}−\mathrm{1}}\int\mathrm{sec}^{{n}−\mathrm{2}} \left(\alpha\right){d}\alpha \\ $$
Answered by sma3l2996 last updated on 18/May/18
![I=∫_0 ^1 t^2 (√(1+t^2 ))dt=∫_0 ^1 t×t(√(1+t^2 ))dt by parts u=t⇒u′=1 v′=t(√(1+t^2 ))⇒v=(1/3)(1+t^2 )(√(1+t^2 )) So I=(1/3)[t(1+t^2 )(√(1+t^2 ))]_0 ^1 −(1/3)∫_0 ^1 (1+t^2 )(√(1+t^2 ))dt I=((2(√2))/3)−(1/3)∫_0 ^1 ((√(1+t^2 ))+t^2 (√(1+t^2 )))dt=((2(√2))/3)−(1/3)∫_0 ^1 (√(1+t^2 ))dt−(1/3)I (4/3)I=((2(√2))/3)−(1/3)∫_0 ^1 (√(1+t^2 ))dt let t=sinh(u)⇒dt=cosh(u)du (√(1+t^2 ))=(√(1+sinh^2 u))=cosh(u) So ∫_0 ^1 (√(1+t^2 ))dt=∫_0 ^(sinh^(−1) (1)) cosh^2 (u)du=(1/2)∫_0 ^(sinh^(−1) (1)) (1+cosh(2u))du =(1/2)[u+(1/2)sinh(2u)]_0 ^(sinh^(−1) (1)) =(1/2)(sinh^(−1) (1)+(√2)) =(1/2)(ln(1+(√2))+(√2)) So I=((√2)/2)−(1/4)((1/2)ln(1+(√2))+((√2)/2)) I=((7(√2))/8)−(1/8)ln(1+(√2))](https://www.tinkutara.com/question/Q35392.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{2}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} {t}×{t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${by}\:{parts} \\ $$$${u}={t}\Rightarrow{u}'=\mathrm{1} \\ $$$${v}'={t}\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\Rightarrow{v}=\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{t}^{\mathrm{2}} } \\ $$$${So}\:\:\:{I}=\frac{\mathrm{1}}{\mathrm{3}}\left[{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{t}^{\mathrm{2}} \right)\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${I}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }+{t}^{\mathrm{2}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }\right){dt}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}−\frac{\mathrm{1}}{\mathrm{3}}{I} \\ $$$$\frac{\mathrm{4}}{\mathrm{3}}{I}=\frac{\mathrm{2}\sqrt{\mathrm{2}}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$${let}\:\:{t}={sinh}\left({u}\right)\Rightarrow{dt}={cosh}\left({u}\right){du} \\ $$$$\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }=\sqrt{\mathrm{1}+{sinh}^{\mathrm{2}} {u}}={cosh}\left({u}\right) \\ $$$${So}\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\mathrm{1}+{t}^{\mathrm{2}} }{dt}=\int_{\mathrm{0}} ^{{sinh}^{−\mathrm{1}} \left(\mathrm{1}\right)} {cosh}^{\mathrm{2}} \left({u}\right){du}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{sinh}^{−\mathrm{1}} \left(\mathrm{1}\right)} \left(\mathrm{1}+{cosh}\left(\mathrm{2}{u}\right)\right){du} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{u}+\frac{\mathrm{1}}{\mathrm{2}}{sinh}\left(\mathrm{2}{u}\right)\right]_{\mathrm{0}} ^{{sinh}^{−\mathrm{1}} \left(\mathrm{1}\right)} =\frac{\mathrm{1}}{\mathrm{2}}\left({sinh}^{−\mathrm{1}} \left(\mathrm{1}\right)+\sqrt{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\sqrt{\mathrm{2}}\right) \\ $$$${So}\:\:{I}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}\left(\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right)+\frac{\sqrt{\mathrm{2}}}{\mathrm{2}}\right) \\ $$$${I}=\frac{\mathrm{7}\sqrt{\mathrm{2}}}{\mathrm{8}}−\frac{\mathrm{1}}{\mathrm{8}}{ln}\left(\mathrm{1}+\sqrt{\mathrm{2}}\right) \\ $$
