Question Number 149944 by ArielVyny last updated on 08/Aug/21
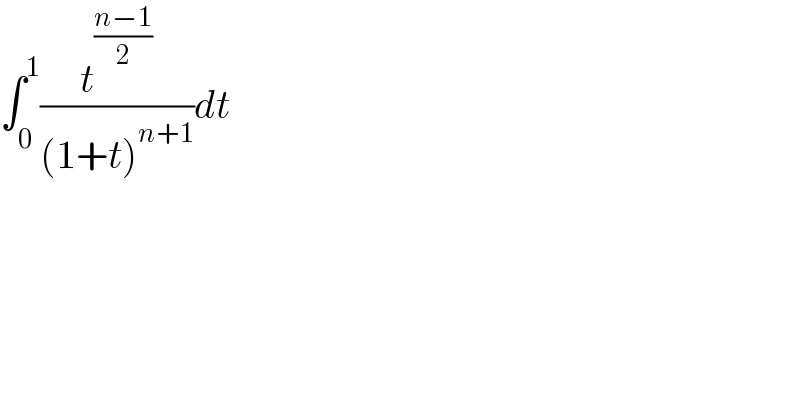
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{t}^{\frac{{n}−\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}+{t}\right)^{{n}+\mathrm{1}} }{dt} \\ $$
Commented by Ar Brandon last updated on 08/Aug/21
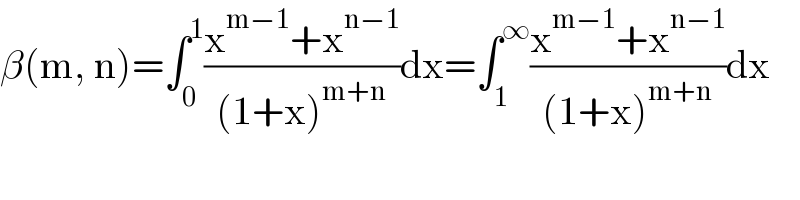
$$\beta\left(\mathrm{m},\:\mathrm{n}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{x}^{\mathrm{m}−\mathrm{1}} +\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{m}+\mathrm{n}} }\mathrm{dx}=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{x}^{\mathrm{m}−\mathrm{1}} +\mathrm{x}^{\mathrm{n}−\mathrm{1}} }{\left(\mathrm{1}+\mathrm{x}\right)^{\mathrm{m}+\mathrm{n}} }\mathrm{dx} \\ $$
