Question Number 103683 by Dwaipayan Shikari last updated on 16/Jul/20
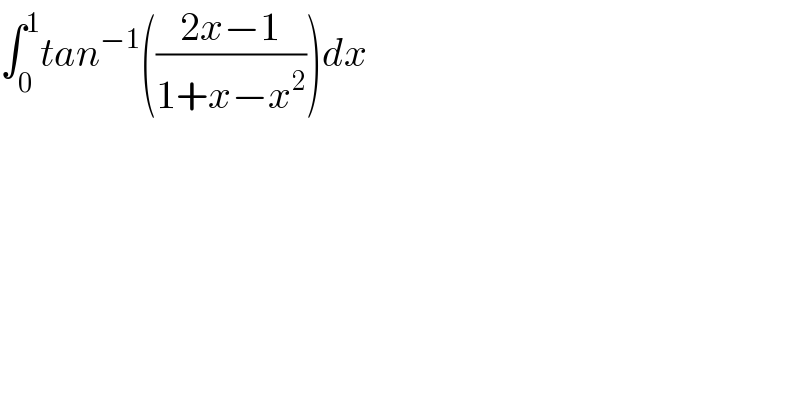
$$\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−\mathrm{1}} \left(\frac{\mathrm{2}{x}−\mathrm{1}}{\mathrm{1}+{x}−{x}^{\mathrm{2}} }\right){dx} \\ $$
Commented by Dwaipayan Shikari last updated on 16/Jul/20
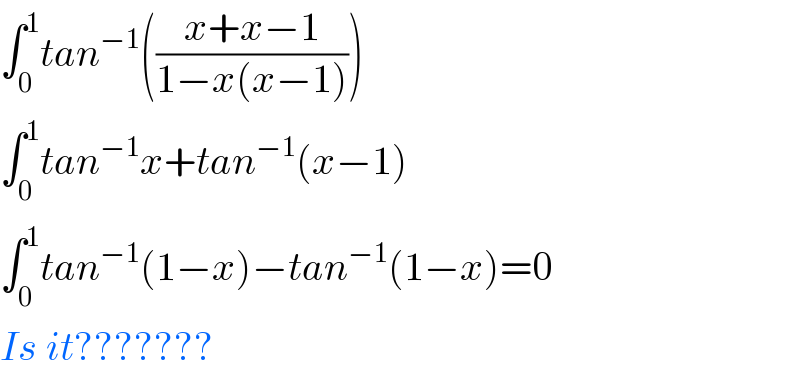
$$\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−\mathrm{1}} \left(\frac{{x}+{x}−\mathrm{1}}{\mathrm{1}−{x}\left({x}−\mathrm{1}\right)}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−\mathrm{1}} {x}+{tan}^{−\mathrm{1}} \left({x}−\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)−{tan}^{−\mathrm{1}} \left(\mathrm{1}−{x}\right)=\mathrm{0} \\ $$$${Is}\:{it}??????? \\ $$
Answered by maths mind last updated on 16/Jul/20
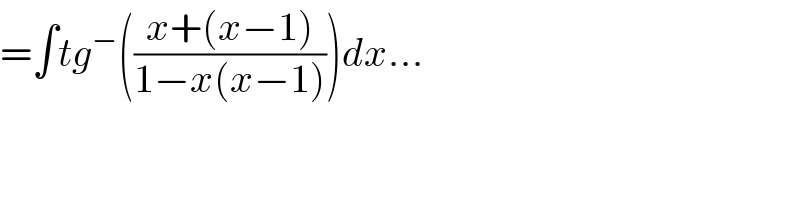
$$=\int{tg}^{−} \left(\frac{{x}+\left({x}−\mathrm{1}\right)}{\mathrm{1}−{x}\left({x}−\mathrm{1}\right)}\right){dx}… \\ $$$$ \\ $$
