0-1-tan-1-x-tan-1-1-x-1-x-2-1-x-1-x-dx-

Question Number 155512 by mathdanisur last updated on 01/Oct/21

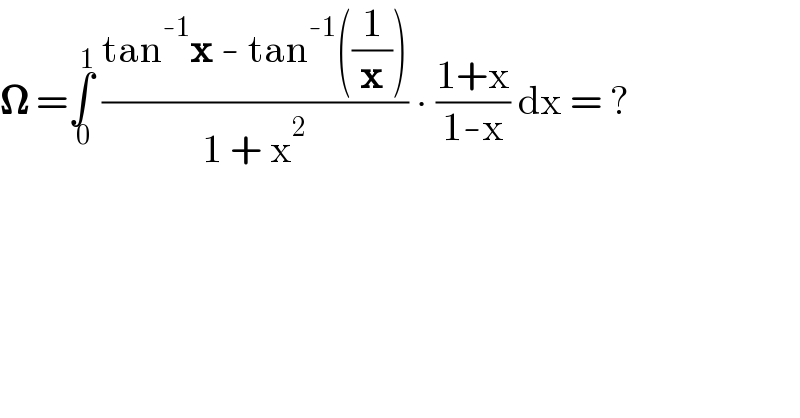
$$\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\frac{\mathrm{tan}^{-\mathrm{1}} \boldsymbol{\mathrm{x}}\:-\:\mathrm{tan}^{-\mathrm{1}} \left(\frac{\mathrm{1}}{\boldsymbol{\mathrm{x}}}\right)}{\mathrm{1}\:+\:\mathrm{x}^{\mathrm{2}} }\:\centerdot\:\frac{\mathrm{1}+\mathrm{x}}{\mathrm{1}-\mathrm{x}}\:\mathrm{dx}\:=\:? \\ $$

Answered by Kamel last updated on 01/Oct/21

Ω=∫_0 ^1 ((Arctan(x)−Arctan((1/x)))/(1+x^2 )) ((1+x)/(1−x))dx =∫_0 ^1 ((Arctan(((x^2 −1)/(2x))))/(1+x^2 )) ((1+x)/(1−x))dx; t=((1−x)/(1+x)) =−2∫_0 ^1 ((Arctan(t))/(t(1+t^2 )))dt=−2∫_0 ^1 ((Arctan(t))/t)dt+2∫_0 ^1 ((tArctan(t))/(1+t^2 ))dt =−2G+(π/4)Ln(2)−∫_0 ^1 ((Ln(1+t^2 ))/(1+t^2 ))dt Ω =−2G+(π/4)Ln(2)+2∫_0 ^(π/4) Ln(cos(x))dx =−2G+(π/4)Ln(2)+2∫_0 ^(π/2) Ln(cos(x))dx−2∫_0 ^(π/4) Ln(sin(x))dx =−2G+(π/4)Ln(2)−πLn(2)+(π/4)Ln(2)+2∫_0 ^(π/4) ((xcos(x))/(sin(x)))dx =^(x=Arctan(t)) −2G−(π/2)Ln(2)+2∫_0 ^1 ((Arctan(t))/(t(1+t^2 )))dt^(=−Ω) ∴ 𝛀=∫_0 ^1 ((Arctan(x)−Arctan((1/x)))/(1+x^2 )) ((1+x)/(1−x))dx=−G−(𝛑/4)Ln(2) KAMEL BENAICHA

$$ \\ $$$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Arctan}\left({x}\right)−{Arctan}\left(\frac{\mathrm{1}}{{x}}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}{dx} \\ $$$$\:\:\:\:=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Arctan}\left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{\mathrm{2}{x}}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }\:\frac{\mathrm{1}+{x}}{\mathrm{1}−{x}}{dx};\:{t}=\frac{\mathrm{1}−{x}}{\mathrm{1}+{x}} \\ $$$$\:\:\:\:=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Arctan}\left({t}\right)}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}=−\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Arctan}\left({t}\right)}{{t}}{dt}+\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{tArctan}\left({t}\right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\:\:\:\:=−\mathrm{2}{G}+\frac{\pi}{\mathrm{4}}{Ln}\left(\mathrm{2}\right)−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Ln}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{\mathrm{1}+{t}^{\mathrm{2}} }{dt} \\ $$$$\:\:\:\Omega\:=−\mathrm{2}{G}+\frac{\pi}{\mathrm{4}}{Ln}\left(\mathrm{2}\right)+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {Ln}\left({cos}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:\:\:\:=−\mathrm{2}{G}+\frac{\pi}{\mathrm{4}}{Ln}\left(\mathrm{2}\right)+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {Ln}\left({cos}\left({x}\right)\right){dx}−\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {Ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$\:\:\:\:\:\:\:\:=−\mathrm{2}{G}+\frac{\pi}{\mathrm{4}}{Ln}\left(\mathrm{2}\right)−\pi{Ln}\left(\mathrm{2}\right)+\frac{\pi}{\mathrm{4}}{Ln}\left(\mathrm{2}\right)+\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \frac{{xcos}\left({x}\right)}{{sin}\left({x}\right)}{dx} \\ $$$$\overset{{x}={Arctan}\left({t}\right)} {=}−\mathrm{2}{G}−\frac{\pi}{\mathrm{2}}{Ln}\left(\mathrm{2}\right)+\overset{=−\Omega} {\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{Arctan}\left({t}\right)}{{t}\left(\mathrm{1}+{t}^{\mathrm{2}} \right)}{dt}} \\ $$$$\therefore\:\:\boldsymbol{\Omega}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{{Arctan}}\left(\boldsymbol{{x}}\right)−\boldsymbol{{Arctan}}\left(\frac{\mathrm{1}}{\boldsymbol{{x}}}\right)}{\mathrm{1}+\boldsymbol{{x}}^{\mathrm{2}} }\:\frac{\mathrm{1}+\boldsymbol{{x}}}{\mathrm{1}−\boldsymbol{{x}}}\boldsymbol{{dx}}=−\boldsymbol{{G}}−\frac{\boldsymbol{\pi}}{\mathrm{4}}\boldsymbol{{Ln}}\left(\mathrm{2}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\boldsymbol{{KAMEL}}\:\boldsymbol{{BENAICHA}} \\ $$

Commented by mathdanisur last updated on 02/Oct/21

$$\mathrm{Very}\:\mathrm{nice}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you} \\ $$

Facebook Tweet Pin

0-1-tan-1-x-tan-1-1-x-1-x-2-1-x-1-x-dx-

Leave a Reply Cancel reply