Menu Close

0-1-tanhx-tanhx-1-5-dx-

Tinku Tara 0 Comments
Pin




Question Number 125708 by Dwaipayan Shikari last updated on 13/Dec/20
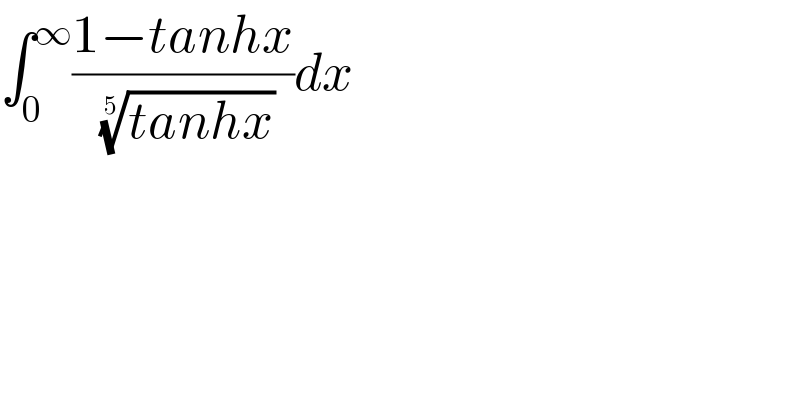
∫_0 ^∞ ((1−tanhx)/( ((tanhx))^(1/5) ))dx
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{tanhx}}{\:\sqrt[{\mathrm{5}}]{{tanhx}}}{dx} \\ $$
Answered by mindispower last updated on 13/Dec/20
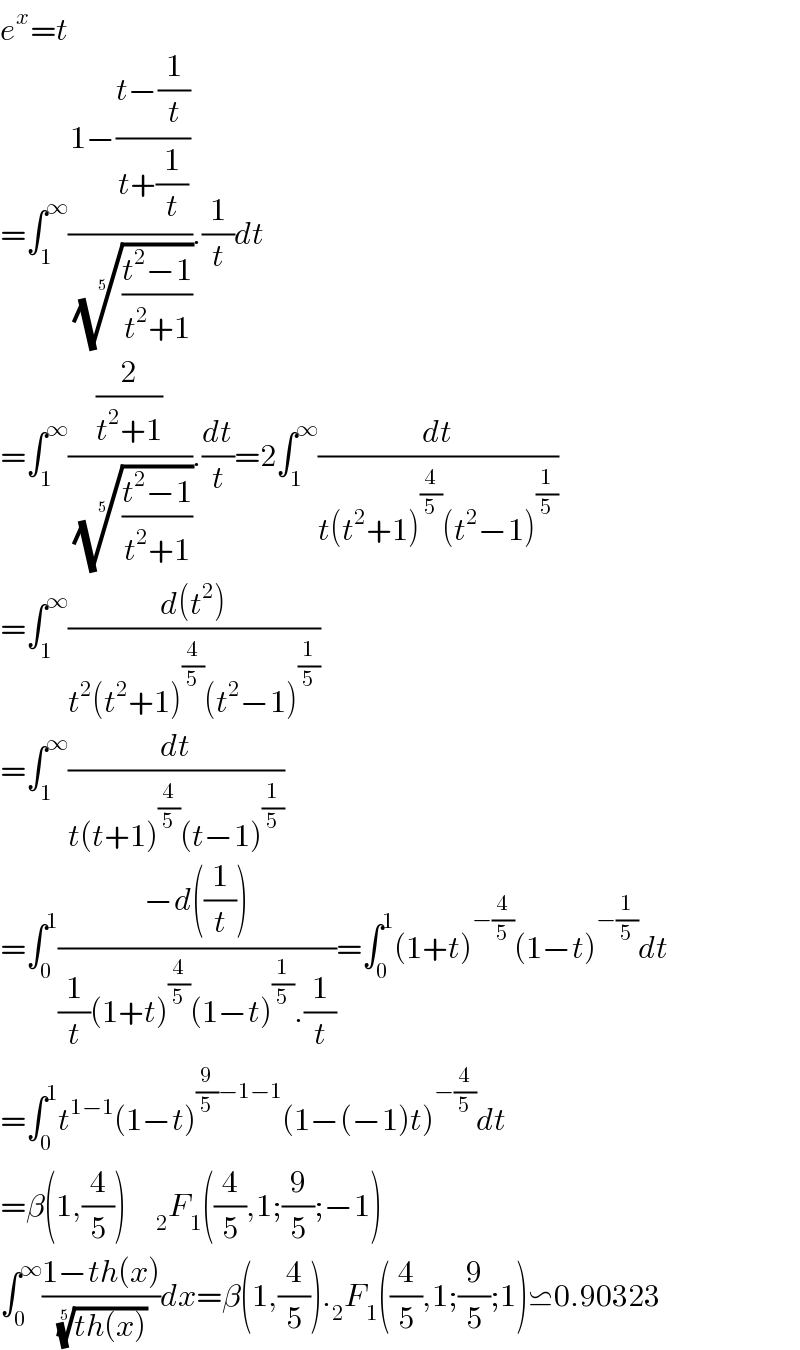
e^x =t =∫_1 ^∞ ((1−((t−(1/t))/(t+(1/t))))/( (((t^2 −1)/(t^2 +1)))^(1/5) )).(1/t)dt =∫_1 ^∞ ((2/(t^2 +1))/( (((t^2 −1)/(t^2 +1)))^(1/5) )).(dt/t)=2∫_1 ^∞ (dt/(t(t^2 +1)^(4/5) (t^2 −1)^(1/5) )) =∫_1 ^∞ ((d(t^2 ))/(t^2 (t^2 +1)^(4/5) (t^2 −1)^(1/5) )) =∫_1 ^∞ (dt/(t(t+1)^(4/5) (t−1)^(1/5) )) =∫_0 ^1 ((−d((1/t)))/((1/t)(1+t)^(4/5) (1−t)^(1/5) .(1/t)))=∫_0 ^1 (1+t)^(−(4/5)) (1−t)^(−(1/5)) dt =∫_0 ^1 t^(1−1) (1−t)^((9/5)−1−1) (1−(−1)t)^(−(4/5)) dt =β(1,(4/5)) _2 F_1 ((4/5),1;(9/5);−1) ∫_0 ^∞ ((1−th(x))/( ((th(x)))^(1/5) ))dx=β(1,(4/5))._2 F_1 ((4/5),1;(9/5);1)⋍0.90323
$${e}^{{x}} ={t} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{\mathrm{1}−\frac{{t}−\frac{\mathrm{1}}{{t}}}{{t}+\frac{\mathrm{1}}{{t}}}}{\:\sqrt[{\mathrm{5}}]{\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}}}.\frac{\mathrm{1}}{{t}}{dt} \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{\frac{\mathrm{2}}{{t}^{\mathrm{2}} +\mathrm{1}}}{\:\sqrt[{\mathrm{5}}]{\frac{{t}^{\mathrm{2}} −\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}}}}.\frac{{dt}}{{t}}=\mathrm{2}\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{5}}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{5}}} } \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{{d}\left({t}^{\mathrm{2}} \right)}{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{5}}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{5}}} }\: \\ $$$$=\int_{\mathrm{1}} ^{\infty} \frac{{dt}}{{t}\left({t}+\mathrm{1}\right)^{\frac{\mathrm{4}}{\mathrm{5}}} \left({t}−\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{5}}} } \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{−{d}\left(\frac{\mathrm{1}}{{t}}\right)}{\frac{\mathrm{1}}{{t}}\left(\mathrm{1}+{t}\right)^{\frac{\mathrm{4}}{\mathrm{5}}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{1}}{\mathrm{5}}} .\frac{\mathrm{1}}{{t}}}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+{t}\right)^{−\frac{\mathrm{4}}{\mathrm{5}}} \left(\mathrm{1}−{t}\right)^{−\frac{\mathrm{1}}{\mathrm{5}}} {dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {t}^{\mathrm{1}−\mathrm{1}} \left(\mathrm{1}−{t}\right)^{\frac{\mathrm{9}}{\mathrm{5}}−\mathrm{1}−\mathrm{1}} \left(\mathrm{1}−\left(−\mathrm{1}\right){t}\right)^{−\frac{\mathrm{4}}{\mathrm{5}}} {dt} \\ $$$$=\beta\left(\mathrm{1},\frac{\mathrm{4}}{\mathrm{5}}\right)\:\:\:\:\:_{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{5}},\mathrm{1};\frac{\mathrm{9}}{\mathrm{5}};−\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{th}\left({x}\right)}{\:\sqrt[{\mathrm{5}}]{{th}\left({x}\right)}}{dx}=\beta\left(\mathrm{1},\frac{\mathrm{4}}{\mathrm{5}}\right)._{\mathrm{2}} {F}_{\mathrm{1}} \left(\frac{\mathrm{4}}{\mathrm{5}},\mathrm{1};\frac{\mathrm{9}}{\mathrm{5}};\mathrm{1}\right)\backsimeq\mathrm{0}.\mathrm{90323} \\ $$
Commented by Dwaipayan Shikari last updated on 13/Dec/20
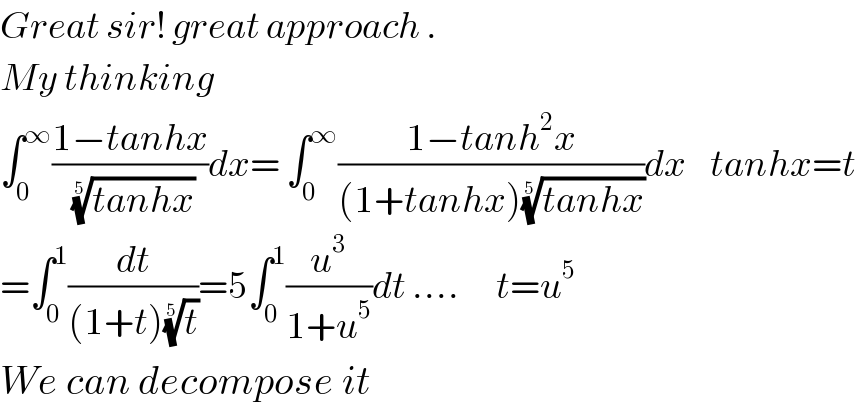
Great sir! great approach . My thinking ∫_0 ^∞ ((1−tanhx)/( ((tanhx))^(1/5) ))dx= ∫_0 ^∞ ((1−tanh^2 x)/((1+tanhx)((tanhx))^(1/5) ))dx tanhx=t =∫_0 ^1 (dt/((1+t)(t)^(1/5) ))=5∫_0 ^1 (u^3 /(1+u^5 ))dt .... t=u^5 We can decompose it
$${Great}\:{sir}!\:{great}\:{approach}\:. \\ $$$${My}\:{thinking} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{tanhx}}{\:\sqrt[{\mathrm{5}}]{{tanhx}}}{dx}=\:\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{tanh}^{\mathrm{2}} {x}}{\left(\mathrm{1}+{tanhx}\right)\sqrt[{\mathrm{5}}]{{tanhx}}}{dx}\:\:\:\:{tanhx}={t} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dt}}{\left(\mathrm{1}+{t}\right)\sqrt[{\mathrm{5}}]{{t}}}=\mathrm{5}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{u}^{\mathrm{3}} }{\mathrm{1}+{u}^{\mathrm{5}} }{dt}\:….\:\:\:\:\:\:{t}={u}^{\mathrm{5}} \: \\ $$$${We}\:{can}\:{decompose}\:{it}\: \\ $$
Commented by mindispower last updated on 13/Dec/20
yes nice nice
$${yes}\:{nice} \\ $$$${nice} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *