Question Number 152105 by talminator2856791 last updated on 25/Aug/21
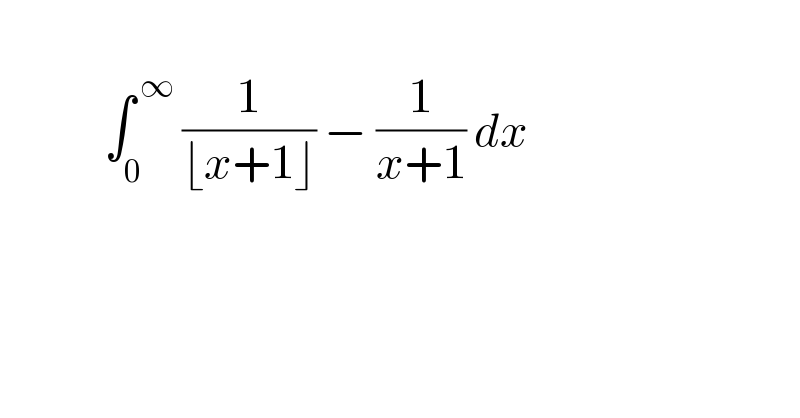
$$\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\frac{\mathrm{1}}{\lfloor{x}+\mathrm{1}\rfloor}\:−\:\frac{\mathrm{1}}{{x}+\mathrm{1}}\:{dx} \\ $$$$\: \\ $$
Answered by Olaf_Thorendsen last updated on 25/Aug/21
![I = ∫_0 ^∞ ((1/(⌊x+1⌋))−(1/(x+1))) dx I = Σ_(n=0) ^∞ ∫_n ^(n+1) ((1/(⌊x+1⌋))−(1/(x+1))) dx I = Σ_(n=0) ^∞ ∫_n ^(n+1) ((1/(n+1))−(1/(x+1))) dx I = Σ_(n=0) ^∞ [(x/(n+1))−ln(x+1)]_n ^(n+1) I = Σ_(n=0) ^∞ ((1/(n+1))−ln(n+2)+ln(n+1)) I = Σ_(n=1) ^∞ ((1/n)−ln(n+1)+ln(n)) Let S_N = Σ_(n=1) ^N ((1/n)−ln(n+1)+ln(n)) S_N = H_N −ln(N+1) H_N = lnN+γ+(1/(2N))−(1/(12N^2 ))+o((1/N^4 )) ⇒ S_N = ln(N/(N+1))+γ+(1/(2N))−(1/(12N^2 ))+o((1/N^4 )) I = lim_(N→∞) S_N = γ I = γ](https://www.tinkutara.com/question/Q152108.png)
$$\mathrm{I}\:=\:\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}}{\lfloor{x}+\mathrm{1}\rfloor}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\:{dx} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{{n}} ^{{n}+\mathrm{1}} \left(\frac{\mathrm{1}}{\lfloor{x}+\mathrm{1}\rfloor}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\:{dx} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{{n}} ^{{n}+\mathrm{1}} \left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{x}+\mathrm{1}}\right)\:{dx} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\frac{{x}}{{n}+\mathrm{1}}−\mathrm{ln}\left({x}+\mathrm{1}\right)\right]_{{n}} ^{{n}+\mathrm{1}} \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}+\mathrm{1}}−\mathrm{ln}\left({n}+\mathrm{2}\right)+\mathrm{ln}\left({n}+\mathrm{1}\right)\right) \\ $$$$\mathrm{I}\:=\:\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\mathrm{ln}\left({n}+\mathrm{1}\right)+\mathrm{ln}\left({n}\right)\right) \\ $$$$\mathrm{Let}\:\mathrm{S}_{\mathrm{N}} \:=\:\underset{{n}=\mathrm{1}} {\overset{\mathrm{N}} {\sum}}\left(\frac{\mathrm{1}}{{n}}−\mathrm{ln}\left({n}+\mathrm{1}\right)+\mathrm{ln}\left({n}\right)\right) \\ $$$$\mathrm{S}_{\mathrm{N}} \:=\:{H}_{\mathrm{N}} −\mathrm{ln}\left(\mathrm{N}+\mathrm{1}\right) \\ $$$${H}_{\mathrm{N}} \:=\:\mathrm{lnN}+\gamma+\frac{\mathrm{1}}{\mathrm{2N}}−\frac{\mathrm{1}}{\mathrm{12N}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{\mathrm{N}^{\mathrm{4}} }\right) \\ $$$$\Rightarrow\:\mathrm{S}_{\mathrm{N}} \:=\:\mathrm{ln}\frac{\mathrm{N}}{\mathrm{N}+\mathrm{1}}+\gamma+\frac{\mathrm{1}}{\mathrm{2N}}−\frac{\mathrm{1}}{\mathrm{12N}^{\mathrm{2}} }+{o}\left(\frac{\mathrm{1}}{\mathrm{N}^{\mathrm{4}} }\right) \\ $$$$\mathrm{I}\:=\:\underset{\mathrm{N}\rightarrow\infty} {\mathrm{lim}}\:\mathrm{S}_{\mathrm{N}} \:=\:\gamma \\ $$$$ \\ $$$$\mathrm{I}\:=\:\gamma \\ $$
