Question Number 163402 by Ahmed777hamouda last updated on 06/Jan/22
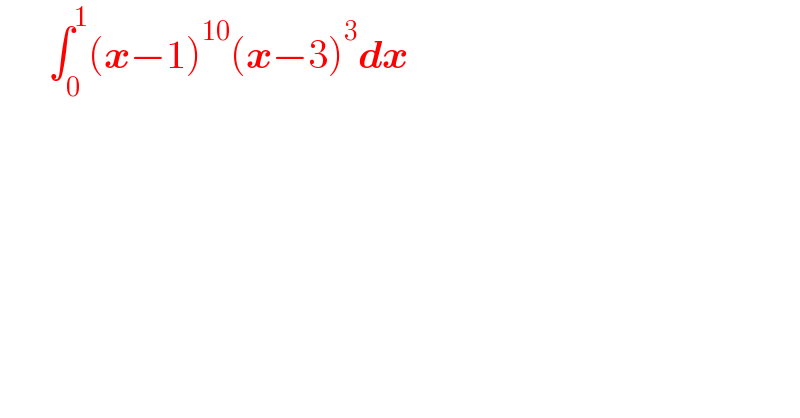
$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\boldsymbol{{x}}−\mathrm{1}\right)^{\mathrm{10}} \left(\boldsymbol{{x}}−\mathrm{3}\right)^{\mathrm{3}} \boldsymbol{{dx}} \\ $$
Answered by Ar Brandon last updated on 06/Jan/22
![I=∫_0 ^1 (x−1)^(10) (x−3)^3 dx, t=x−3 =∫_(−3) ^(−2) (t+2)^(10) t^3 dt=[((t^3 (t+2)^(11) )/(11))]_(−3) ^(−2) −(3/(11))∫_(−3) ^(−2) t^2 (t+2)^(11) dt =−((27)/(11))−(3/(11))[((t^2 (t+2)^(12) )/(12))]_(−3) ^(−2) +(3/(11))∙(2/(12))∫_(−3) ^(−2) t(t+2)^(12) dt =−((27)/(11))+((27)/(11×12))+(1/(22))[((t(t+2)^(13) )/(13))]_(−3) ^(−2) −(1/(22))∙(1/(13))∫_(−3) ^(−2) (t+2)^(13) dt =−((27)/(11))+((27)/(132))−(1/(22))∙(3/(13))−(1/(22×13))∙[(((t+2)^(14) )/(14))]_(−3) ^(−2) =−((27)/(11))+((27)/(132))−(3/(286))−(1/(286×14))=−((4525)/(2002))](https://www.tinkutara.com/question/Q163406.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}−\mathrm{1}\right)^{\mathrm{10}} \left({x}−\mathrm{3}\right)^{\mathrm{3}} {dx},\:{t}={x}−\mathrm{3} \\ $$$$\:\:\:=\int_{−\mathrm{3}} ^{−\mathrm{2}} \left({t}+\mathrm{2}\right)^{\mathrm{10}} {t}^{\mathrm{3}} {dt}=\left[\frac{{t}^{\mathrm{3}} \left({t}+\mathrm{2}\right)^{\mathrm{11}} }{\mathrm{11}}\right]_{−\mathrm{3}} ^{−\mathrm{2}} −\frac{\mathrm{3}}{\mathrm{11}}\int_{−\mathrm{3}} ^{−\mathrm{2}} {t}^{\mathrm{2}} \left({t}+\mathrm{2}\right)^{\mathrm{11}} {dt} \\ $$$$\:\:\:=−\frac{\mathrm{27}}{\mathrm{11}}−\frac{\mathrm{3}}{\mathrm{11}}\left[\frac{{t}^{\mathrm{2}} \left({t}+\mathrm{2}\right)^{\mathrm{12}} }{\mathrm{12}}\right]_{−\mathrm{3}} ^{−\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{11}}\centerdot\frac{\mathrm{2}}{\mathrm{12}}\int_{−\mathrm{3}} ^{−\mathrm{2}} {t}\left({t}+\mathrm{2}\right)^{\mathrm{12}} {dt} \\ $$$$\:\:\:=−\frac{\mathrm{27}}{\mathrm{11}}+\frac{\mathrm{27}}{\mathrm{11}×\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{22}}\left[\frac{{t}\left({t}+\mathrm{2}\right)^{\mathrm{13}} }{\mathrm{13}}\right]_{−\mathrm{3}} ^{−\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{22}}\centerdot\frac{\mathrm{1}}{\mathrm{13}}\int_{−\mathrm{3}} ^{−\mathrm{2}} \left({t}+\mathrm{2}\right)^{\mathrm{13}} {dt} \\ $$$$\:\:\:=−\frac{\mathrm{27}}{\mathrm{11}}+\frac{\mathrm{27}}{\mathrm{132}}−\frac{\mathrm{1}}{\mathrm{22}}\centerdot\frac{\mathrm{3}}{\mathrm{13}}−\frac{\mathrm{1}}{\mathrm{22}×\mathrm{13}}\centerdot\left[\frac{\left({t}+\mathrm{2}\right)^{\mathrm{14}} }{\mathrm{14}}\right]_{−\mathrm{3}} ^{−\mathrm{2}} \\ $$$$\:\:\:=−\frac{\mathrm{27}}{\mathrm{11}}+\frac{\mathrm{27}}{\mathrm{132}}−\frac{\mathrm{3}}{\mathrm{286}}−\frac{\mathrm{1}}{\mathrm{286}×\mathrm{14}}=−\frac{\mathrm{4525}}{\mathrm{2002}} \\ $$
Commented by peter frank last updated on 07/Jan/22

$$\mathrm{great} \\ $$
