Question Number 160204 by amin96 last updated on 25/Nov/21
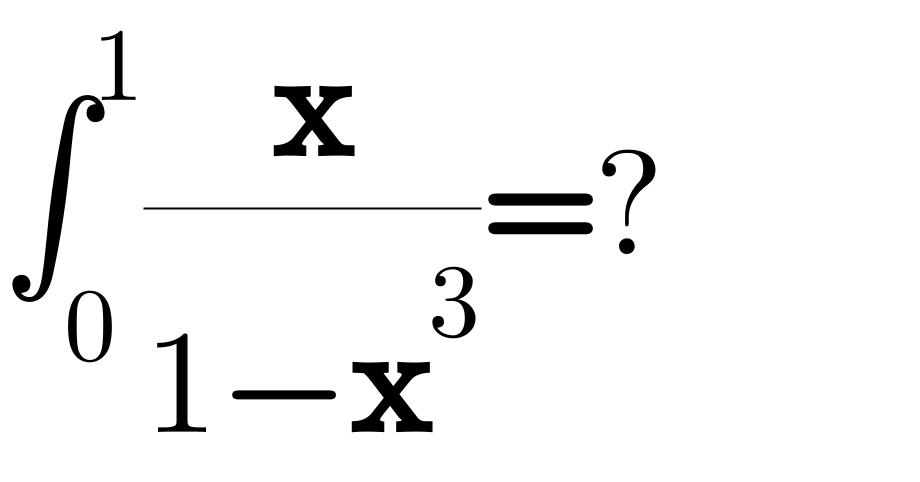
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\boldsymbol{\mathrm{x}}}{\mathrm{1}−\boldsymbol{\mathrm{x}}^{\mathrm{3}} }=? \\ $$
Commented by mr W last updated on 25/Nov/21
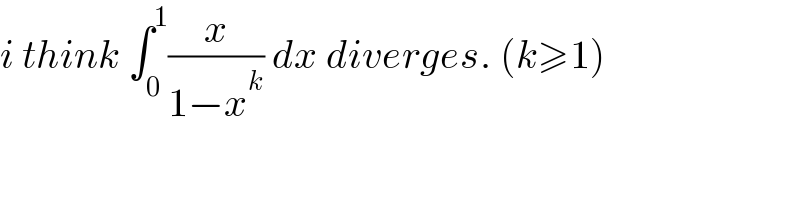
$${i}\:{think}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\mathrm{1}−{x}^{{k}} }\:{dx}\:{diverges}.\:\left({k}\geqslant\mathrm{1}\right) \\ $$
Answered by Ar Brandon last updated on 25/Nov/21
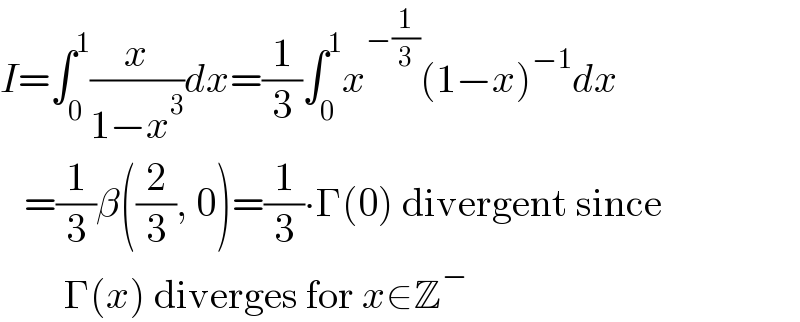
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\mathrm{1}−{x}^{\mathrm{3}} }{dx}=\frac{\mathrm{1}}{\mathrm{3}}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{−\frac{\mathrm{1}}{\mathrm{3}}} \left(\mathrm{1}−{x}\right)^{−\mathrm{1}} {dx} \\ $$$$\:\:\:=\frac{\mathrm{1}}{\mathrm{3}}\beta\left(\frac{\mathrm{2}}{\mathrm{3}},\:\mathrm{0}\right)=\frac{\mathrm{1}}{\mathrm{3}}\centerdot\Gamma\left(\mathrm{0}\right)\:\mathrm{divergent}\:\mathrm{since} \\ $$$$\:\:\:\:\:\:\:\:\Gamma\left({x}\right)\:\mathrm{diverges}\:\mathrm{for}\:{x}\in\mathbb{Z}^{−} \\ $$
