Question Number 97552 by bemath last updated on 08/Jun/20
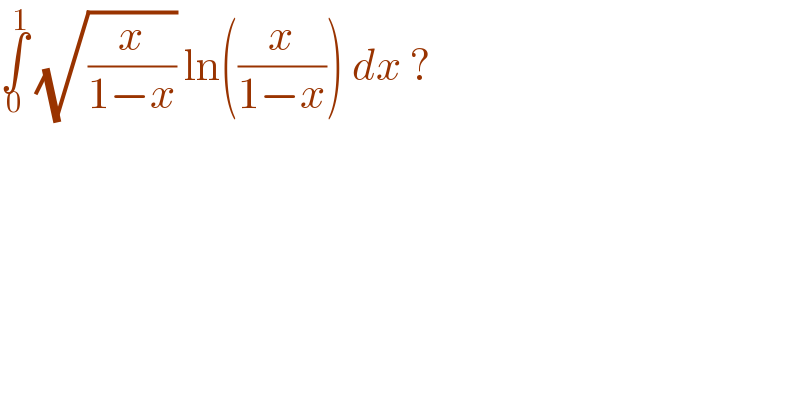
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt{\frac{{x}}{\mathrm{1}−{x}}}\:\mathrm{ln}\left(\frac{{x}}{\mathrm{1}−{x}}\right)\:{dx}\:? \\ $$
Answered by john santu last updated on 08/Jun/20
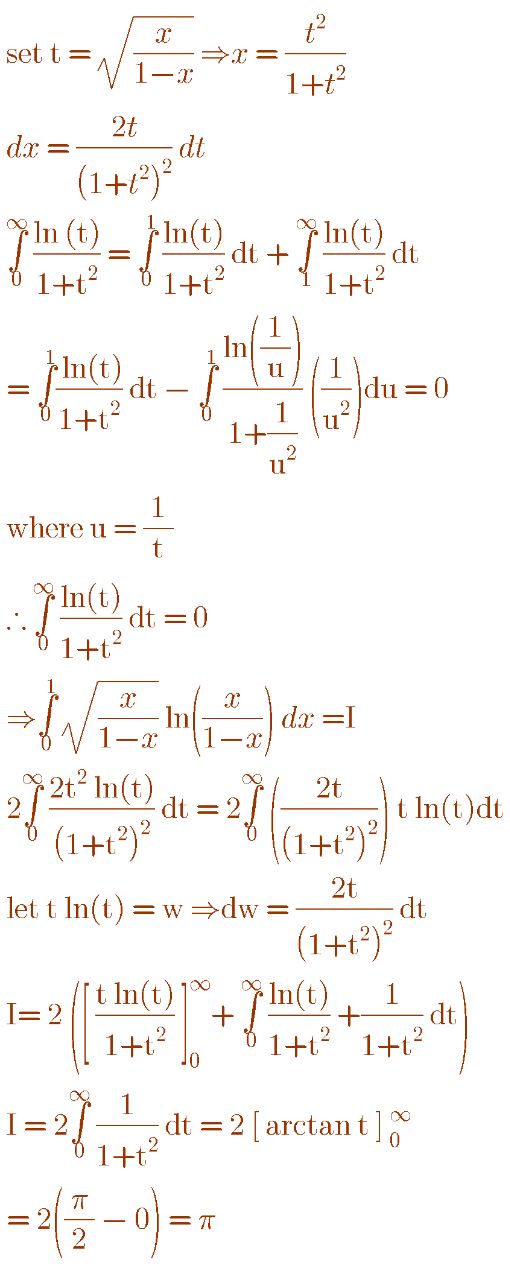
Answered by abdomathmax last updated on 08/Jun/20
![let I =∫_0 ^1 (√(x/(1−x)))ln((x/(1−x)))dx changement (√(x/(1−x)))=t give (x/(1−x)) =t^2 ⇒x =t^2 −t^2 x ⇒(1+t^2 )x =t^2 ⇒ x =(t^2 /(1+t^2 )) =((1+t^2 −1)/(1+t^2 )) =1−(1/(1+t^2 )) ⇒(dx/dt) =((2t)/((1+t^2 )^2 )) ⇒ I =∫_0 ^∞ t ln(((t^2 /(1+t^2 ))/(1−(t^2 /(1+t^2 )))))((2t)/((1+t^2 )^2 ))dt =4 ∫_0 ^∞ (t^2 /((1+t^2 )^2 ))ln(t)dt =4 ∫_0 ^∞ ((1+t^2 −1)/((1+t^2 )^2 ))ln(t)dt =4 ∫_0 ^∞ ((lnt)/(1+t^2 ))dt−4∫_0 ^∞ ((lnt)/((1+t^2 )^2 ))dt =0−4 ∫_0 ^∞ ((lnt)/((1+t^2 )^2 ))dt let A =∫_0 ^∞ ((lnt)/((1+t^2 )^2 ))dt ⇒A =∫_0 ^1 ((lnt)/((1+t^2 )^2 ))dt+∫_1 ^(+∞) ((lnt)/((1+t^2 )^2 ))dt ∫_1 ^(+∞) ((lnt)/((1+t^2 )^2 ))dt =_(t=(1/u)) ∫_0 ^1 ((lnu)/((1+(1/u^2 ))^2 ))×((−du)/u^2 ) =−∫_0 ^1 ((u^2 lnu)/((1+u^2 )^2 ))du ⇒A =∫_0 ^1 (((1−t^2 )lnt)/((1+t^2 )^2 ))dt (1/(1+u)) =Σ_(n=0) ^∞ (−1)^n u^n ⇒ −(1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^n u^(n−1) ⇒ (1/((1+u)^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) u^(n−1) ⇒ (1/((1+x^2 )^2 )) =Σ_(n=1) ^∞ n(−1)^(n−1) x^(2n−2) ⇒ A =∫_0 ^1 (1−x^2 )lnx(Σ_(n=1) ^∞ n(−1)^(n−1) x^(2n−2) )dx =Σ_(n=1) ^∞ n(−1)^(n−1) ∫_0 ^1 (x^(2n−2) −x^(2n) )lnxdx w_n =∫_0 ^1 (x^(2n−2) −x^(2n) )ln(x)dx =[((1/(2n−1))x^(2n−1) −(1/(2n+1))x^(2n+1) )lnx]_0 ^1 −∫_0 ^1 ((1/(2n−1))x^(2n−2) −(1/(2n+1))x^(2n) )dx =−(1/((2n−1)^2 )) +(1/((2n+1)^2 )) ⇒ A =Σ_(n=1) ^∞ n(−1)^(n−1) ((1/((2n+1)^2 ))−(1/((2n−1)^2 ))) =Σ_(n=1) ^∞ (n/((2n+1)^2 ))(−1)^(n−1) −Σ_(n=1) ^∞ ((n(−1)^(n−1) )/((2n−1)^2 ))(→n=p+1) =Σ_(n=1) ^∞ (n/((2n+1)^2 ))(−1)^(n−1) −Σ_(p=0) ^∞ (((p+1)(−1)^p )/((2p+1)^2 )) =−Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) −Σ_(n=1) ^∞ (((n+1)(−1)^n )/((2n+1)^2 )) −1 =−2 Σ_(n=1) ^∞ ((n(−1)^n )/((2n+1)^2 )) −Σ_(n=1) ^∞ (((−1)^n )/((2n+1)^2 ))−1 rest to find those sums ...be continued...](https://www.tinkutara.com/question/Q97595.png)
$$\mathrm{let}\:\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\sqrt{\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}}}\mathrm{ln}\left(\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}}\right)\mathrm{dx}\:\mathrm{changement}\:\sqrt{\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}}}=\mathrm{t} \\ $$$$\mathrm{give}\:\frac{\mathrm{x}}{\mathrm{1}−\mathrm{x}}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow\mathrm{x}\:=\mathrm{t}^{\mathrm{2}} −\mathrm{t}^{\mathrm{2}} \mathrm{x}\:\Rightarrow\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)\mathrm{x}\:=\mathrm{t}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{x}\:=\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\:\Rightarrow\frac{\mathrm{dx}}{\mathrm{dt}}\:=\frac{\mathrm{2t}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\:\mathrm{t}\:\mathrm{ln}\left(\frac{\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}{\mathrm{1}−\frac{\mathrm{t}^{\mathrm{2}} }{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\right)\frac{\mathrm{2t}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt} \\ $$$$=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}+\mathrm{t}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{t}\right)\mathrm{dt}\:=\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\mathrm{dt}−\mathrm{4}\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$=\mathrm{0}−\mathrm{4}\:\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\mathrm{let}\:\mathrm{A}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\:\Rightarrow\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}+\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\int_{\mathrm{1}} ^{+\infty} \:\frac{\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt}\:=_{\mathrm{t}=\frac{\mathrm{1}}{\mathrm{u}}} \:\:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{lnu}}{\left(\mathrm{1}+\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\right)^{\mathrm{2}} }×\frac{−\mathrm{du}}{\mathrm{u}^{\mathrm{2}} } \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{u}^{\mathrm{2}} \mathrm{lnu}}{\left(\mathrm{1}+\mathrm{u}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{du}\:\Rightarrow\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)\mathrm{lnt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{dt} \\ $$$$\frac{\mathrm{1}}{\mathrm{1}+\mathrm{u}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}} \:\Rightarrow \\ $$$$−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} \:\mathrm{u}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{u}^{\mathrm{n}−\mathrm{1}} \:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{A}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{lnx}\left(\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{x}^{\mathrm{2n}−\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{x}^{\mathrm{2n}−\mathrm{2}} −\mathrm{x}^{\mathrm{2n}} \right)\mathrm{lnxdx} \\ $$$$\mathrm{w}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\mathrm{x}^{\mathrm{2n}−\mathrm{2}} −\mathrm{x}^{\mathrm{2n}} \right)\mathrm{ln}\left(\mathrm{x}\right)\mathrm{dx} \\ $$$$=\left[\left(\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}\mathrm{x}^{\mathrm{2n}−\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{x}^{\mathrm{2n}+\mathrm{1}} \right)\mathrm{lnx}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$−\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\frac{\mathrm{1}}{\mathrm{2n}−\mathrm{1}}\mathrm{x}^{\mathrm{2n}−\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{2n}+\mathrm{1}}\mathrm{x}^{\mathrm{2n}} \right)\mathrm{dx} \\ $$$$=−\frac{\mathrm{1}}{\left(\mathrm{2n}−\mathrm{1}\right)^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:\Rightarrow \\ $$$$\mathrm{A}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \left(\frac{\mathrm{1}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{1}}{\left(\mathrm{2n}−\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} }{\left(\mathrm{2n}−\mathrm{1}\right)^{\mathrm{2}} }\left(\rightarrow\mathrm{n}=\mathrm{p}+\mathrm{1}\right) \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}}{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:−\sum_{\mathrm{p}=\mathrm{0}} ^{\infty} \:\frac{\left(\mathrm{p}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{p}} }{\left(\mathrm{2p}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$=−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(\mathrm{n}+\mathrm{1}\right)\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\mathrm{1} \\ $$$$=−\mathrm{2}\:\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{n}\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }\:−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\left(−\mathrm{1}\right)^{\mathrm{n}} }{\left(\mathrm{2n}+\mathrm{1}\right)^{\mathrm{2}} }−\mathrm{1} \\ $$$$\mathrm{rest}\:\mathrm{to}\:\mathrm{find}\:\mathrm{those}\:\mathrm{sums}\:…\mathrm{be}\:\mathrm{continued}… \\ $$
