Menu Close

0-1-x-1-x-x-2-2-ln-ln-1-x-dx-3-1-3-ln-6-3-pi-pi-3-27-5ln2pi-6ln-1-6-

Tinku Tara 0 Comments
Pin




Question Number 152142 by Ar Brandon last updated on 26/Aug/21
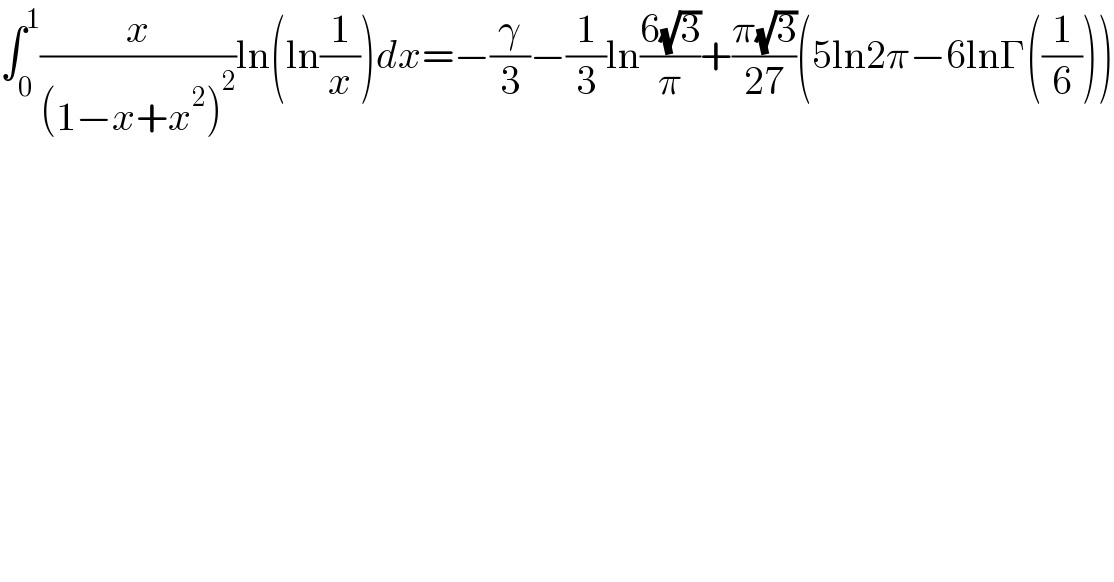
∫_0 ^1 (x/((1−x+x^2 )^2 ))ln(ln(1/x))dx=−(γ/3)−(1/3)ln((6(√3))/π)+((π(√3))/(27))(5ln2π−6lnΓ((1/6)))
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\left(\mathrm{1}−{x}+{x}^{\mathrm{2}} \right)^{\mathrm{2}} }\mathrm{ln}\left(\mathrm{ln}\frac{\mathrm{1}}{{x}}\right){dx}=−\frac{\gamma}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{ln}\frac{\mathrm{6}\sqrt{\mathrm{3}}}{\pi}+\frac{\pi\sqrt{\mathrm{3}}}{\mathrm{27}}\left(\mathrm{5ln2}\pi−\mathrm{6ln}\Gamma\left(\frac{\mathrm{1}}{\mathrm{6}}\right)\right) \\ $$
Answered by mindispower last updated on 28/Aug/21
∫_0 ^∞ ((e^(−2t) ln(t)dt)/((1−e^(−t) +e^(−2t) )^2 )) ∫_0 ^∞ ((t^s e^(−2t) )/((1−e^(−t) +e^(−2t) )^2 ))dt f(s)=∫_0 ^∞ ((t^s e^(−2t) (1+2e^(−t) +e^(−2t) ))/((1+e^(−3t) )^2 ))dt =Σ_(m≥0) (−1)^m .m∫_0 ^∞ t^s (e^(−t(2+3m)) +e^(−t(3+3m)) +e^(−t(4+3m)) )dt =Σ_(m≥0) (−1)^m .mΓ(1+s)((1/((2+3m)^(s+1) ))+(1/((3+3m)^(s+1) ))+(1/((4+3m)^(s+1) ))) =((Γ(1+s))/3^(s+1) )Σ_(m≥1) (−1)^m .m((1/((m+(2/3))^(s+1) ))+(1/((1+m)^(s+1) ))+(1/((m+(4/3))^(s+1) ))) =((Γ(1+s))/3^(s+1) )Σ_(m≥0) (−1)^m ((1/((m+(2/3))^s ))+(1/((1+m)^s ))+(1/((m+(4/3))^s )) −(2/(3(m+(2/3))^(s+1) ))−(1/((1+m)^(s+1) ))−(4/(3(m+(4/3))^(s+1) ))) =((Γ(1+s))/3^(s+1) )Σ_(m≥0) (ζ((1/3),s)−ζ((5/6),s)+η(s)−η(1+s) +ζ((2/3),s)−ζ((7/6),s)−(2/3)(ζ((1/3),s+1)−ζ((5/6),s+1)) −(4/3)(ζ((2/3),1+s)−ζ((7/6),1+s)) we want ,f′(0) too bee continuede too many calculation just using steiljes constante of laurent expesion zeta hurwitz fomction
$$\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−\mathrm{2}{t}} {ln}\left({t}\right){dt}}{\left(\mathrm{1}−{e}^{−{t}} +{e}^{−\mathrm{2}{t}} \right)^{\mathrm{2}} } \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{s}} {e}^{−\mathrm{2}{t}} }{\left(\mathrm{1}−{e}^{−{t}} +{e}^{−\mathrm{2}{t}} \right)^{\mathrm{2}} }{dt} \\ $$$${f}\left({s}\right)=\int_{\mathrm{0}} ^{\infty} \frac{{t}^{{s}} {e}^{−\mathrm{2}{t}} \left(\mathrm{1}+\mathrm{2}{e}^{−{t}} +{e}^{−\mathrm{2}{t}} \right)}{\left(\mathrm{1}+{e}^{−\mathrm{3}{t}} \right)^{\mathrm{2}} }{dt} \\ $$$$=\underset{{m}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{m}} .{m}\int_{\mathrm{0}} ^{\infty} {t}^{{s}} \left({e}^{−{t}\left(\mathrm{2}+\mathrm{3}{m}\right)} +{e}^{−{t}\left(\mathrm{3}+\mathrm{3}{m}\right)} +{e}^{−{t}\left(\mathrm{4}+\mathrm{3}{m}\right)} \right){dt} \\ $$$$=\underset{{m}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\overset{{m}} {\right)}.{m}\Gamma\left(\mathrm{1}+{s}\right)\left(\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{3}{m}\right)^{{s}+\mathrm{1}} }+\frac{\mathrm{1}}{\left(\mathrm{3}+\mathrm{3}{m}\right)^{{s}+\mathrm{1}} }+\frac{\mathrm{1}}{\left(\mathrm{4}+\mathrm{3}{m}\right)^{{s}+\mathrm{1}} }\right) \\ $$$$=\frac{\Gamma\left(\mathrm{1}+{s}\right)}{\mathrm{3}^{{s}+\mathrm{1}} }\underset{{m}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{m}} .{m}\left(\frac{\mathrm{1}}{\left({m}+\frac{\mathrm{2}}{\mathrm{3}}\right)^{{s}+\mathrm{1}} }+\frac{\mathrm{1}}{\left(\mathrm{1}+{m}\right)^{{s}+\mathrm{1}} }+\frac{\mathrm{1}}{\left({m}+\frac{\mathrm{4}}{\mathrm{3}}\right)^{{s}+\mathrm{1}} }\right) \\ $$$$=\frac{\Gamma\left(\mathrm{1}+{s}\right)}{\mathrm{3}^{{s}+\mathrm{1}} }\underset{{m}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{m}} \left(\frac{\mathrm{1}}{\left({m}+\frac{\mathrm{2}}{\mathrm{3}}\right)^{{s}} }+\frac{\mathrm{1}}{\left(\mathrm{1}+{m}\right)^{{s}} }+\frac{\mathrm{1}}{\left({m}+\frac{\mathrm{4}}{\mathrm{3}}\right)^{{s}} }\right. \\ $$$$\left.−\frac{\mathrm{2}}{\mathrm{3}\left({m}+\frac{\mathrm{2}}{\mathrm{3}}\right)^{{s}+\mathrm{1}} }−\frac{\mathrm{1}}{\left(\mathrm{1}+{m}\right)^{{s}+\mathrm{1}} }−\frac{\mathrm{4}}{\mathrm{3}\left({m}+\frac{\mathrm{4}}{\mathrm{3}}\right)^{{s}+\mathrm{1}} }\right) \\ $$$$=\frac{\Gamma\left(\mathrm{1}+{s}\right)}{\mathrm{3}^{{s}+\mathrm{1}} }\underset{{m}\geqslant\mathrm{0}} {\sum}\left(\zeta\left(\frac{\mathrm{1}}{\mathrm{3}},{s}\right)−\zeta\left(\frac{\mathrm{5}}{\mathrm{6}},{s}\right)+\eta\left({s}\right)−\eta\left(\mathrm{1}+{s}\right)\right. \\ $$$$+\zeta\left(\frac{\mathrm{2}}{\mathrm{3}},{s}\right)−\zeta\left(\frac{\mathrm{7}}{\mathrm{6}},{s}\right)−\frac{\mathrm{2}}{\mathrm{3}}\left(\zeta\left(\frac{\mathrm{1}}{\mathrm{3}},{s}+\mathrm{1}\right)−\zeta\left(\frac{\mathrm{5}}{\mathrm{6}},{s}+\mathrm{1}\right)\right) \\ $$$$−\frac{\mathrm{4}}{\mathrm{3}}\left(\zeta\left(\frac{\mathrm{2}}{\mathrm{3}},\mathrm{1}+{s}\right)−\zeta\left(\frac{\mathrm{7}}{\mathrm{6}},\mathrm{1}+{s}\right)\right) \\ $$$${we}\:{want}\:,{f}'\left(\mathrm{0}\right) \\ $$$${too}\:{bee}\:{continuede}\:{too}\:{many}\:{calculation} \\ $$$$\:{just}\:{using}\:{steiljes}\:{constante} \\ $$$${of}\:{laurent}\:{expesion}\:{zeta}\:{hurwitz}\:{fomction} \\ $$
Commented by Ar Brandon last updated on 28/Aug/21
wow thanks sir
$$\mathrm{wow}\:\mathrm{thanks}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *