Menu Close

0-1-x-10-1-dx-2pi-5-5-1-pi-5-

Tinku Tara 0 Comments
Pin




Question Number 96034 by  M±th+et+s last updated on 29/May/20
∫_0 ^∞ (1/(x^(10) +1))dx=((2π)/(5((√5)−1)))=((πφ)/5)
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{{x}^{\mathrm{10}} +\mathrm{1}}{dx}=\frac{\mathrm{2}\pi}{\mathrm{5}\left(\sqrt{\mathrm{5}}−\mathrm{1}\right)}=\frac{\pi\phi}{\mathrm{5}} \\ $$
Commented by  M±th+et+s last updated on 30/May/20
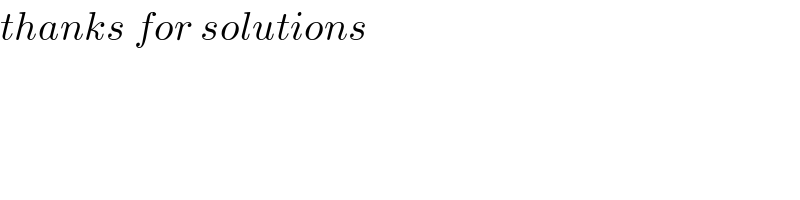
thanks for solutions
$${thanks}\:{for}\:{solutions} \\ $$
Answered by abdomathmax last updated on 29/May/20
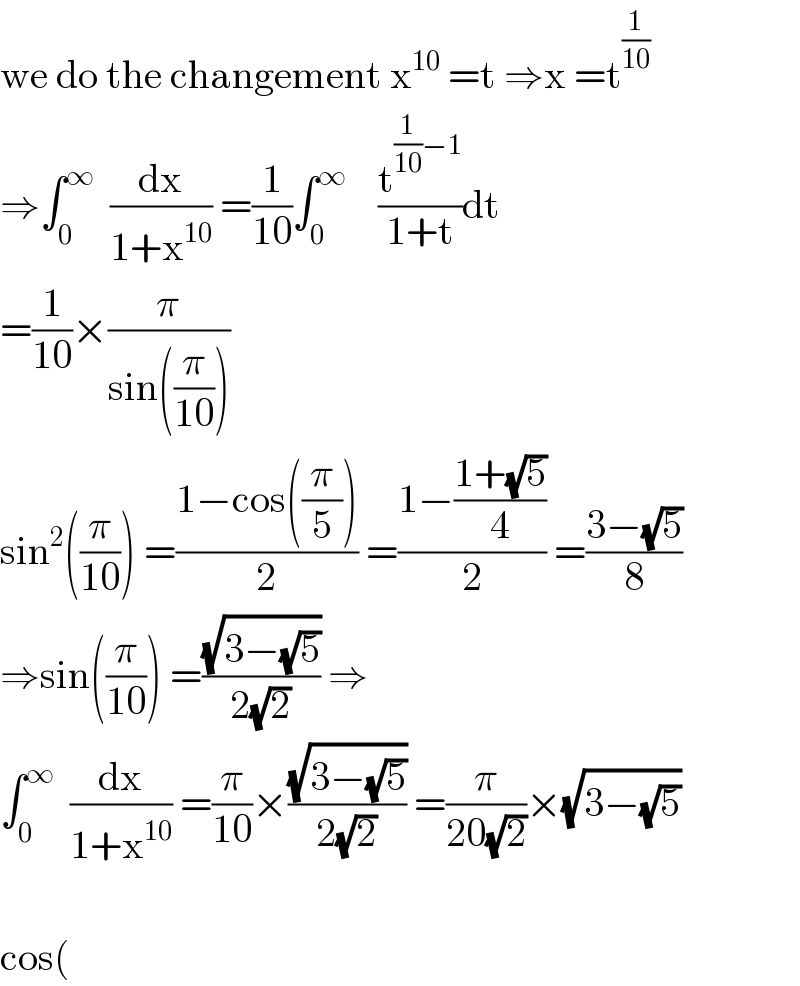
we do the changement x^(10) =t ⇒x =t^(1/(10)) ⇒∫_0 ^∞ (dx/(1+x^(10) )) =(1/(10))∫_0 ^∞ (t^((1/(10))−1) /(1+t))dt =(1/(10))×(π/(sin((π/(10))))) sin^2 ((π/(10))) =((1−cos((π/5)))/2) =((1−((1+(√5))/4))/2) =((3−(√5))/8) ⇒sin((π/(10))) =((√(3−(√5)))/(2(√2))) ⇒ ∫_0 ^∞ (dx/(1+x^(10) )) =(π/(10))×((√(3−(√5)))/(2(√2))) =(π/(20(√2)))×(√(3−(√5))) cos(
$$\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\mathrm{x}^{\mathrm{10}} \:=\mathrm{t}\:\Rightarrow\mathrm{x}\:=\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{10}}} \\ $$$$\Rightarrow\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{10}} }\:=\frac{\mathrm{1}}{\mathrm{10}}\int_{\mathrm{0}} ^{\infty} \:\:\:\:\frac{\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{10}}−\mathrm{1}} }{\mathrm{1}+\mathrm{t}}\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}×\frac{\pi}{\mathrm{sin}\left(\frac{\pi}{\mathrm{10}}\right)} \\ $$$$\mathrm{sin}^{\mathrm{2}} \left(\frac{\pi}{\mathrm{10}}\right)\:=\frac{\mathrm{1}−\mathrm{cos}\left(\frac{\pi}{\mathrm{5}}\right)}{\mathrm{2}}\:=\frac{\mathrm{1}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{4}}}{\mathrm{2}}\:=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$\Rightarrow\mathrm{sin}\left(\frac{\pi}{\mathrm{10}}\right)\:=\frac{\sqrt{\mathrm{3}−\sqrt{\mathrm{5}}}}{\mathrm{2}\sqrt{\mathrm{2}}}\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{dx}}{\mathrm{1}+\mathrm{x}^{\mathrm{10}} }\:=\frac{\pi}{\mathrm{10}}×\frac{\sqrt{\mathrm{3}−\sqrt{\mathrm{5}}}}{\mathrm{2}\sqrt{\mathrm{2}}}\:=\frac{\pi}{\mathrm{20}\sqrt{\mathrm{2}}}×\sqrt{\mathrm{3}−\sqrt{\mathrm{5}}} \\ $$$$ \\ $$$$\mathrm{cos}\left(\right. \\ $$
Answered by Sourav mridha last updated on 29/May/20
∫_0 ^∞ (1/(1+(x^5 )^2 ))dx substitute (x^5 ) by tan Φ and after little manipulation you get =(1/5)∫_0 ^(𝛑/2) (sin𝚽)^(−(4/5)) .(cos Φ)^(4/5) dΦ =(1/(10))((Γ((1/(10))).Γ((9/(10))))/(Γ(1)))=(1/(10))Γ((1/(10)))Γ(1−(1/(10))) =(1/(10)) (π/(sin ((π/(10))))) now putting the value of( sin(18^° )) =(((√5) −1)/4)..we get ∫_0 ^∞ (1/(x^(10) +1))dx=((2𝛑)/(5((√5) −1)))=((𝛑∅)/5)
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\mathrm{1}+\left(\mathrm{x}^{\mathrm{5}} \right)^{\mathrm{2}} }\mathrm{dx}\:\mathrm{substitute}\:\left(\mathrm{x}^{\mathrm{5}} \right)\:\mathrm{by}\:\mathrm{tan}\:\Phi \\ $$$$\mathrm{and}\:\mathrm{after}\:\mathrm{little}\:\mathrm{manipulation}\:\mathrm{you}\:\mathrm{get} \\ $$$$=\frac{\mathrm{1}}{\mathrm{5}}\int_{\mathrm{0}} ^{\frac{\boldsymbol{\pi}}{\mathrm{2}}} \left(\boldsymbol{{sin}\Phi}\right)^{−\frac{\mathrm{4}}{\mathrm{5}}} .\left(\mathrm{cos}\:\Phi\right)^{\frac{\mathrm{4}}{\mathrm{5}}} \mathrm{d}\Phi \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}}\frac{\Gamma\left(\frac{\mathrm{1}}{\mathrm{10}}\right).\Gamma\left(\frac{\mathrm{9}}{\mathrm{10}}\right)}{\Gamma\left(\mathrm{1}\right)}=\frac{\mathrm{1}}{\mathrm{10}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{10}}\right)\Gamma\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\mathrm{10}}\:\frac{\pi}{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{10}}\right)} \\ $$$$\mathrm{now}\:\mathrm{putting}\:\mathrm{the}\:\mathrm{value}\:\mathrm{of}\left(\:\mathrm{sin}\left(\mathrm{18}^{°} \right)\right)\: \\ $$$$=\frac{\sqrt{\mathrm{5}}\:−\mathrm{1}}{\mathrm{4}}..\mathrm{we}\:\mathrm{get} \\ $$$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}}{\boldsymbol{{x}}^{\mathrm{10}} +\mathrm{1}}\boldsymbol{{dx}}=\frac{\mathrm{2}\boldsymbol{\pi}}{\mathrm{5}\left(\sqrt{\mathrm{5}}\:−\mathrm{1}\right)}=\frac{\boldsymbol{\pi}\emptyset}{\mathrm{5}} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *