Question Number 107264 by Dwaipayan Shikari last updated on 09/Aug/20

$$\int_{\mathrm{0}} ^{\infty} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Aug/20

Answered by mr W last updated on 09/Aug/20
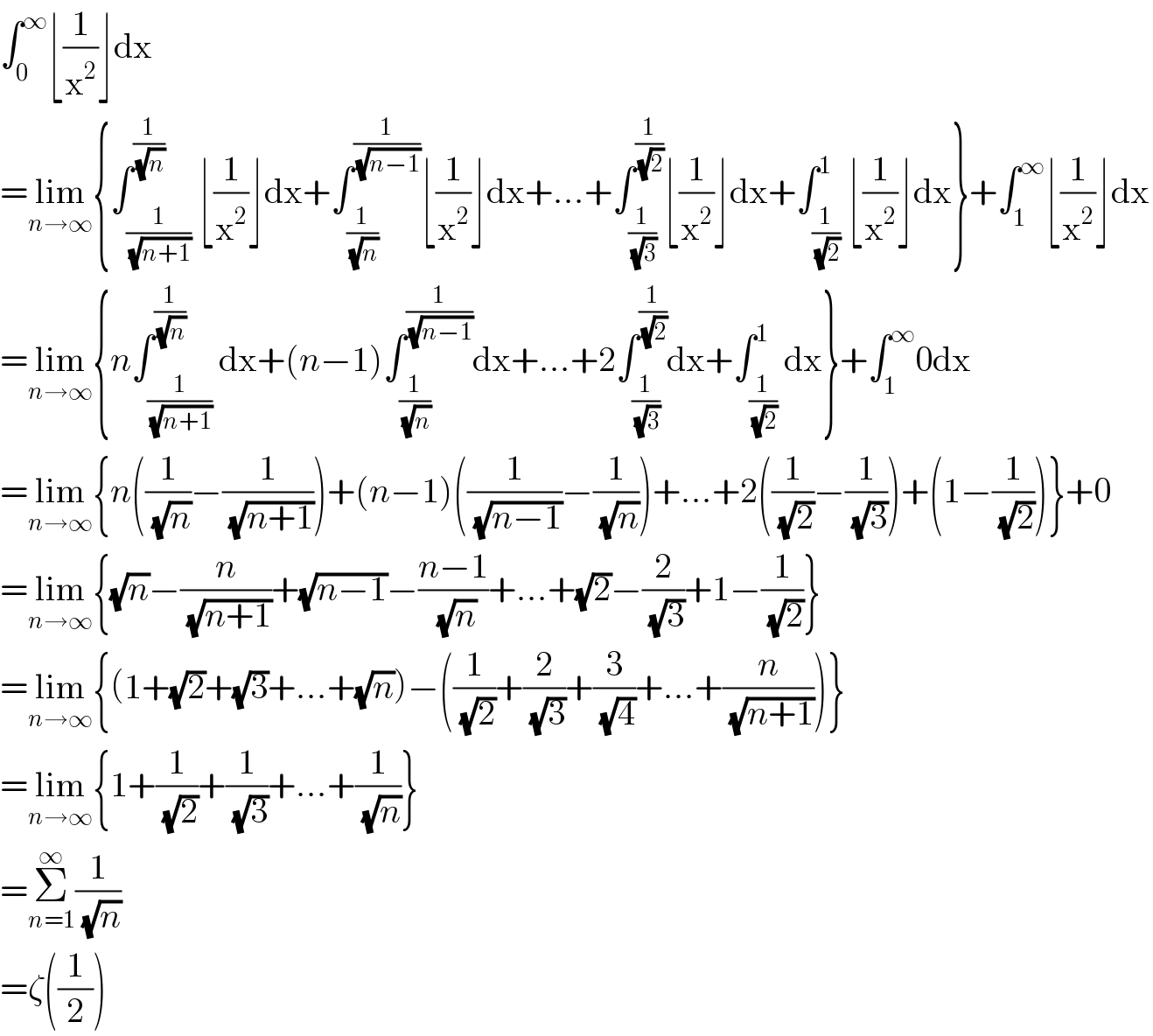
$$\int_{\mathrm{0}} ^{\infty} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\int_{\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}}} ^{\frac{\mathrm{1}}{\:\sqrt{{n}}}} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx}+\int_{\frac{\mathrm{1}}{\:\sqrt{{n}}}} ^{\frac{\mathrm{1}}{\:\sqrt{{n}−\mathrm{1}}}} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx}+…+\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx}+\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx}\right\}+\int_{\mathrm{1}} ^{\infty} \lfloor\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\rfloor\mathrm{dx} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{{n}\int_{\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}}} ^{\frac{\mathrm{1}}{\:\sqrt{{n}}}} \mathrm{dx}+\left({n}−\mathrm{1}\right)\int_{\frac{\mathrm{1}}{\:\sqrt{{n}}}} ^{\frac{\mathrm{1}}{\:\sqrt{{n}−\mathrm{1}}}} \mathrm{dx}+…+\mathrm{2}\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}} ^{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} \mathrm{dx}+\int_{\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}} ^{\mathrm{1}} \mathrm{dx}\right\}+\int_{\mathrm{1}} ^{\infty} \mathrm{0dx} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{{n}\left(\frac{\mathrm{1}}{\:\sqrt{{n}}}−\frac{\mathrm{1}}{\:\sqrt{{n}+\mathrm{1}}}\right)+\left({n}−\mathrm{1}\right)\left(\frac{\mathrm{1}}{\:\sqrt{{n}−\mathrm{1}}}−\frac{\mathrm{1}}{\:\sqrt{{n}}}\right)+…+\mathrm{2}\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}\right)+\left(\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right)\right\}+\mathrm{0} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\sqrt{{n}}−\frac{{n}}{\:\sqrt{{n}+\mathrm{1}}}+\sqrt{{n}−\mathrm{1}}−\frac{{n}−\mathrm{1}}{\:\sqrt{{n}}}+…+\sqrt{\mathrm{2}}−\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}+\mathrm{1}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}\right\} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\left(\mathrm{1}+\sqrt{\mathrm{2}}+\sqrt{\mathrm{3}}+…+\sqrt{{n}}\right)−\left(\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{2}}{\:\sqrt{\mathrm{3}}}+\frac{\mathrm{3}}{\:\sqrt{\mathrm{4}}}+…+\frac{{n}}{\:\sqrt{{n}+\mathrm{1}}}\right)\right\} \\ $$$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left\{\mathrm{1}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{2}}}+\frac{\mathrm{1}}{\:\sqrt{\mathrm{3}}}+…+\frac{\mathrm{1}}{\:\sqrt{{n}}}\right\} \\ $$$$=\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\:\sqrt{{n}}} \\ $$$$=\zeta\left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$
Commented by mr W last updated on 09/Aug/20

$${yes} \\ $$
Commented by Dwaipayan Shikari last updated on 09/Aug/20

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}\:\mathrm{diverges} \\ $$
Answered by mathmax by abdo last updated on 09/Aug/20
![I =∫_0 ^∞ [(1/x^2 )]dx we do the changement (1/x^2 )=t ⇒x^2 =(1/t) ⇒x=(1/( (√t))) so I =−∫_0 ^∞ [t](−(1/(2t(√t))))dt =(1/2)∫_0 ^∞ (([t])/(t(√t))) dt =(1/2)Σ_(n=0) ^∞ ∫_n ^(n+1) (n/(t(√t)))dt =(1/2)Σ_(n=0) ^∞ n ∫_n ^(n+1) (dt/t^(3/2) ) =(1/2)Σ_(n=0) ^∞ n∫_n ^(n+1) t^(−(3/2)) dt =(1/2)Σ_(n=0) ^∞ n×[(1/(−(3/2)+1)) t^(−(3/2)+1) ]_n ^(n+1) =−Σ_(n=0) ^∞ n{(1/( (√(n+1))))−(1/( (√n)))} =Σ_(n=0) ^∞ (√n)−Σ_(n=0) ^∞ (n/( (√(n+1)))) =Σ_(n=0) ^∞ (√n)−Σ_(n=0) ^∞ ((n+1−1)/( (√(n+1)))) =Σ_(n=0) ^∞ (√n)−Σ_(n=0) ^∞ (√(n+1))+Σ_(n=0) ^∞ (1/( (√(n+1)))) =Σ_(n=1) ^∞ (√n)−Σ_(n=1) ^∞ (√n)+ Σ_(n=0) ^∞ (1/( (√(n+1)))) =Σ_(n=1) ^∞ (1/( (√n))) =+∞ ⇒ so I diverge to +∞](https://www.tinkutara.com/question/Q107280.png)
$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\infty} \:\left[\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\right]\mathrm{dx}\:\:\mathrm{we}\:\mathrm{do}\:\mathrm{the}\:\mathrm{changement}\:\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }=\mathrm{t}\:\Rightarrow\mathrm{x}^{\mathrm{2}} \:=\frac{\mathrm{1}}{\mathrm{t}}\:\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{t}}} \\ $$$$\mathrm{so}\:\mathrm{I}\:=−\int_{\mathrm{0}} ^{\infty} \:\left[\mathrm{t}\right]\left(−\frac{\mathrm{1}}{\mathrm{2t}\sqrt{\mathrm{t}}}\right)\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\infty} \:\:\:\frac{\left[\mathrm{t}\right]}{\mathrm{t}\sqrt{\mathrm{t}}}\:\mathrm{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{n}}{\mathrm{t}\sqrt{\mathrm{t}}}\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{n}\:\int_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \:\frac{\mathrm{dt}}{\mathrm{t}^{\frac{\mathrm{3}}{\mathrm{2}}} } \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{n}\int_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \:\mathrm{t}^{−\frac{\mathrm{3}}{\mathrm{2}}} \:\mathrm{dt}\:=\frac{\mathrm{1}}{\mathrm{2}}\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{n}×\left[\frac{\mathrm{1}}{−\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}}\:\mathrm{t}^{−\frac{\mathrm{3}}{\mathrm{2}}+\mathrm{1}} \right]_{\mathrm{n}} ^{\mathrm{n}+\mathrm{1}} \\ $$$$=−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \mathrm{n}\left\{\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}+\mathrm{1}}}−\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\right\}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \sqrt{\mathrm{n}}−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{n}}{\:\sqrt{\mathrm{n}+\mathrm{1}}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \sqrt{\mathrm{n}}−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{n}+\mathrm{1}−\mathrm{1}}{\:\sqrt{\mathrm{n}+\mathrm{1}}}\:=\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\sqrt{\mathrm{n}}−\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \sqrt{\mathrm{n}+\mathrm{1}}+\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}+\mathrm{1}}} \\ $$$$=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \sqrt{\mathrm{n}}−\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \sqrt{\mathrm{n}}+\:\sum_{\mathrm{n}=\mathrm{0}} ^{\infty} \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}+\mathrm{1}}}\:=\sum_{\mathrm{n}=\mathrm{1}} ^{\infty} \:\frac{\mathrm{1}}{\:\sqrt{\mathrm{n}}}\:=+\infty\:\Rightarrow \\ $$$$\mathrm{so}\:\mathrm{I}\:\mathrm{diverge}\:\mathrm{to}\:+\infty \\ $$
