0-1-x-2-log-1-x-dx-

Question Number 113159 by Dwaipayan Shikari last updated on 11/Sep/20

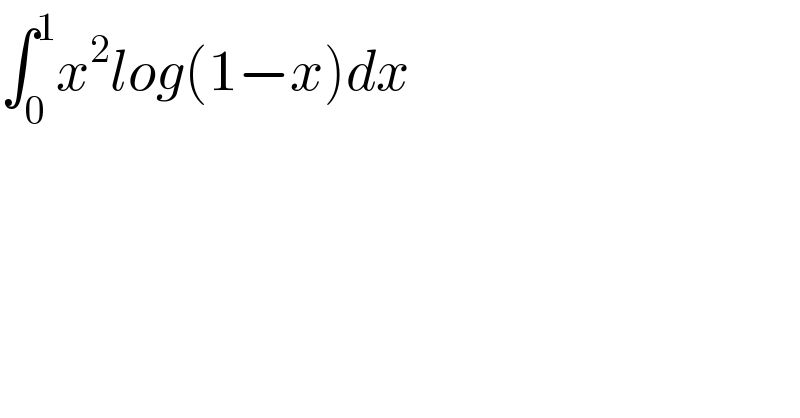
\int_{0}^{1} x^{2} l o g (1 - x) d x

Answered by MJS_new last updated on 11/Sep/20

\int x^{2} \ln (1 - x) d x =

[by parts]

= \frac{x^{3}}{3} \ln (1 - x) - \frac{1}{3} \int \frac{x^{3}}{x - 1} d x =

= \frac{x^{3}}{3} \ln (1 - x) - \frac{1}{3} \int x^{2} + x + 1 + \frac{1}{x - 1} d x =

= \frac{x^{3}}{3} \ln (1 - x) - \frac{1}{3} \ln (x - 1) - \frac{x^{3}}{9} - \frac{x^{2}}{6} - \frac{x}{3} + C

now we have to calculate the limit of this

with x \to 1^{-}

I get \underset{0}{\int^{1}} x^{2} \ln (1 - x) d x = - \frac{11}{18}

Commented by Dwaipayan Shikari last updated on 11/Sep/20

I {h a v e n}^{'} t t h o u g h t o f t h i s . T h a n k i n g y o u

Answered by abdomsup last updated on 11/Sep/20

l e t A = \int_{0}^{1} x^{2} l n (1 - x) d x w e h a v e

\frac{d}{d x} l n (1 - x) = - \frac{1}{1 - x} = - \sum_{n = 0}^{\infty} x^{n}

\Rightarrow l n (1 - x) = - \sum_{n = 0}^{\infty} \frac{x^{n + 1}}{n + 1}

= - \sum_{n = 1}^{\infty} \frac{x^{n}}{n} \Rightarrow

A = - \int_{0}^{1} x^{2} (\sum_{n = 1}^{\infty} \frac{x^{n}}{n}) d x

= - \sum_{n = 1}^{\infty} \frac{1}{n} \int_{0}^{1} x^{n + 2} d x

= - \sum_{n = 1}^{\infty} \frac{1}{n (n + 3)}

= - \frac{1}{3} \sum_{n = 1}^{\infty} (\frac{1}{n} - \frac{1}{n + 3})

= - \frac{1}{3} \sum_{n = 1}^{\infty} \frac{1}{n} + \frac{1}{3} \sum_{n = 1}^{\infty} \frac{1}{n + 3}

b u t \sum_{n = 1}^{\infty} \frac{1}{n + 3} = \sum_{n = 4}^{\infty} \frac{1}{n} \Rightarrow

A = - \frac{1}{3} {1 + \frac{1}{2} + \frac{1}{3} + \sum_{n = 4}^{\infty} \frac{1}{n}}

+ \frac{1}{3} \sum_{n = 4}^{\infty} \frac{1}{4} = - \frac{1}{3} {\frac{3}{2} + \frac{1}{3}}

= - \frac{1}{2} - \frac{1}{9} = \frac{- 11}{18}

Commented by Dwaipayan Shikari last updated on 11/Sep/20

G r e a t s i r!