Question Number 144245 by ArielVyny last updated on 23/Jun/21

$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}{n}} }{\left({x}−\mathrm{1}\right)^{{n}} }{dx} \\ $$
Answered by mathmax by abdo last updated on 23/Jun/21
![A_n =∫_0 ^1 (x^(2n) /((x−1)^n ))dx changement x−1=−t give A_n =∫_1 ^0 (((1−t)^(2n) )/((−t)^n ))(−dt) =(−1)^(n ) ∫_0 ^1 (((1−t)^(2n) )/t^n )dt =(−1)^n ∫_0 ^1 ((Σ_(k=0) ^(2n) C_(2n) ^k t^k (−1)^(2n−k) )/t^n )dt =(−1)^n Σ_(k=0) ^(2n) (−1)^k C_(2n) ^k ∫_0 ^1 t^(k−n) dt =(−1)^n Σ_(k=0 andk≠n−1) ^(2n) (−1)^k C_(2n) ^(k ) ×(1/(k−n+1)) +(−1)^n (−1)^(n−1) C_(2n) ^(n−1) [logt]_0 ^1 so this integral is not convergent..!(exept n=0)](https://www.tinkutara.com/question/Q144247.png)
$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{x}^{\mathrm{2n}} }{\left(\mathrm{x}−\mathrm{1}\right)^{\mathrm{n}} }\mathrm{dx}\:\mathrm{changement}\:\mathrm{x}−\mathrm{1}=−\mathrm{t}\:\mathrm{give} \\ $$$$\mathrm{A}_{\mathrm{n}} =\int_{\mathrm{1}} ^{\mathrm{0}} \:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2n}} }{\left(−\mathrm{t}\right)^{\mathrm{n}} }\left(−\mathrm{dt}\right)\:=\left(−\mathrm{1}\right)^{\mathrm{n}\:} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2n}} }{\mathrm{t}^{\mathrm{n}} }\mathrm{dt} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\mathrm{C}_{\mathrm{2n}} ^{\mathrm{k}} \:\mathrm{t}^{\mathrm{k}} \left(−\mathrm{1}\right)^{\mathrm{2n}−\mathrm{k}} }{\mathrm{t}^{\mathrm{n}} }\mathrm{dt} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{2n}} ^{\mathrm{k}} \int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{t}^{\mathrm{k}−\mathrm{n}} \:\mathrm{dt} \\ $$$$=\left(−\mathrm{1}\right)^{\mathrm{n}} \:\sum_{\mathrm{k}=\mathrm{0}\:\mathrm{andk}\neq\mathrm{n}−\mathrm{1}} ^{\mathrm{2n}} \:\left(−\mathrm{1}\right)^{\mathrm{k}} \:\mathrm{C}_{\mathrm{2n}} ^{\mathrm{k}\:} \:×\frac{\mathrm{1}}{\mathrm{k}−\mathrm{n}+\mathrm{1}} \\ $$$$+\left(−\mathrm{1}\right)^{\mathrm{n}} \:\left(−\mathrm{1}\right)^{\mathrm{n}−\mathrm{1}} \:\mathrm{C}_{\mathrm{2n}} ^{\mathrm{n}−\mathrm{1}} \:\left[\mathrm{logt}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$\mathrm{so}\:\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{not}\:\mathrm{convergent}..!\left(\mathrm{exept}\:\mathrm{n}=\mathrm{0}\right) \\ $$
Commented by ArielVyny last updated on 24/Jun/21

$${look}\:{at}\:{this}\:{Mr} \\ $$
Answered by ArielVyny last updated on 24/Jun/21
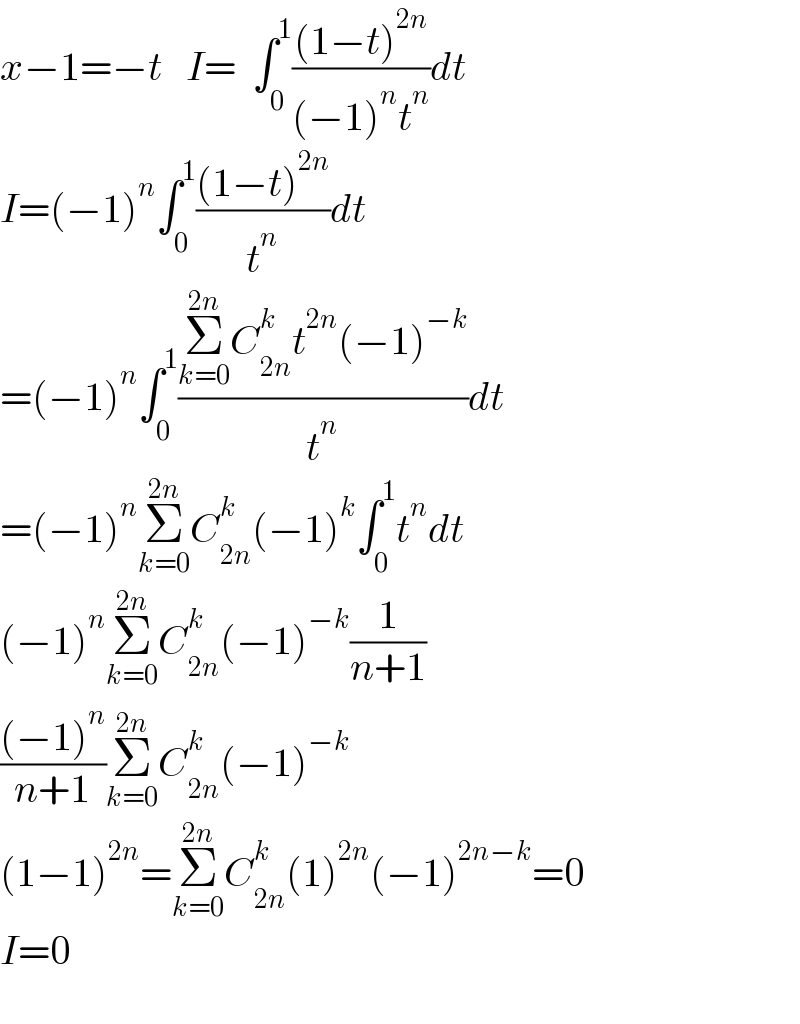
$${x}−\mathrm{1}=−{t}\:\:\:{I}=\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{t}\right)^{\mathrm{2}{n}} }{\left(−\mathrm{1}\right)^{{n}} {t}^{{n}} }{dt} \\ $$$${I}=\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{t}\right)^{\mathrm{2}{n}} }{{t}^{{n}} }{dt} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} {t}^{\mathrm{2}{n}} \left(−\mathrm{1}\right)^{−{k}} }{{t}^{{n}} }{dt} \\ $$$$=\left(−\mathrm{1}\right)^{{n}} \underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} \left(−\mathrm{1}\right)^{{k}} \int_{\mathrm{0}} ^{\mathrm{1}} {t}^{{n}} {dt} \\ $$$$\left(−\mathrm{1}\right)^{{n}} \underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} \left(−\mathrm{1}\right)^{−{k}} \frac{\mathrm{1}}{{n}+\mathrm{1}} \\ $$$$\frac{\left(−\mathrm{1}\right)^{{n}} }{{n}+\mathrm{1}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} \left(−\mathrm{1}\right)^{−{k}} \\ $$$$\left(\mathrm{1}−\mathrm{1}\right)^{\mathrm{2}{n}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{2}{n}} {\sum}}{C}_{\mathrm{2}{n}} ^{{k}} \left(\mathrm{1}\right)^{\mathrm{2}{n}} \left(−\mathrm{1}\right)^{\mathrm{2}{n}−{k}} =\mathrm{0} \\ $$$${I}=\mathrm{0} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 25/Jun/21
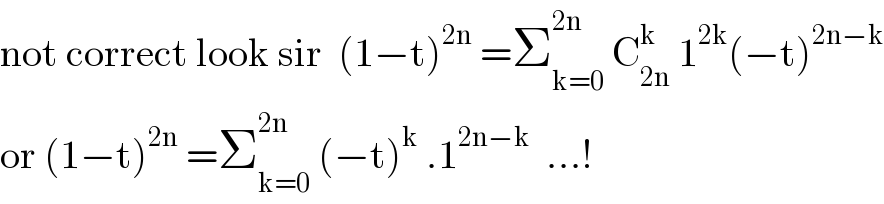
$$\mathrm{not}\:\mathrm{correct}\:\mathrm{look}\:\mathrm{sir}\:\:\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2n}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\mathrm{C}_{\mathrm{2n}} ^{\mathrm{k}} \:\mathrm{1}^{\mathrm{2k}} \left(−\mathrm{t}\right)^{\mathrm{2n}−\mathrm{k}} \\ $$$$\mathrm{or}\:\left(\mathrm{1}−\mathrm{t}\right)^{\mathrm{2n}} \:=\sum_{\mathrm{k}=\mathrm{0}} ^{\mathrm{2n}} \:\left(−\mathrm{t}\right)^{\mathrm{k}} \:.\mathrm{1}^{\mathrm{2n}−\mathrm{k}} \:\:…! \\ $$
