Question Number 52944 by Tawa1 last updated on 15/Jan/19
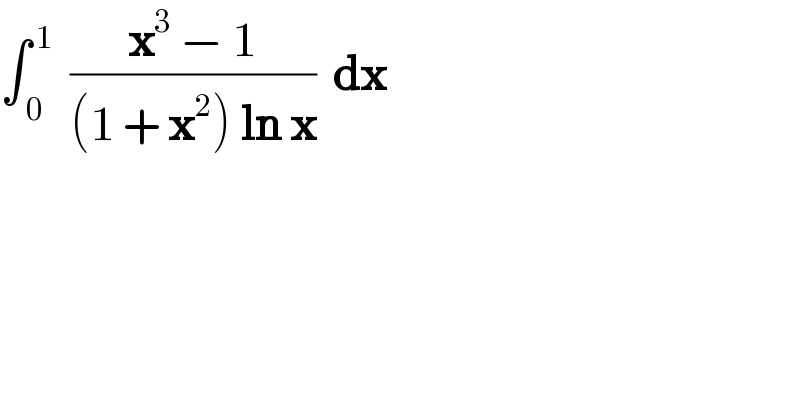
$$\int_{\:\mathrm{0}} ^{\:\mathrm{1}} \:\:\frac{\boldsymbol{\mathrm{x}}^{\mathrm{3}} \:−\:\mathrm{1}}{\left(\mathrm{1}\:+\:\boldsymbol{\mathrm{x}}^{\mathrm{2}} \right)\:\boldsymbol{\mathrm{ln}}\:\boldsymbol{\mathrm{x}}}\:\:\boldsymbol{\mathrm{dx}} \\ $$
Answered by tanmay.chaudhury50@gmail.com last updated on 15/Jan/19
![I(a)=∫_0 ^1 ((x^a −1)/(1+x^2 ))×(dx/(lnx)) (dI_ /da)=∫_0 ^1 (∂/∂a)(((x^a −1)/(1+x^2 )))×(dx/(lnx)) =∫_0 ^1 ((x^a lnx)/(1+x^2 ))×(dx/(lnx)) =∫_0 ^1 (x^a /(1+x^2 ))dx =∫_0 ^1 x^a (1−x^2 +x^4 −x^6 +...)dx =∫_0 ^1 x^a −x^(2+a) +x^(4+a) −x^(6+a) +...dx =∣(x^(a+1) /(a+1))−(x^(a+3) /(a+3))−(x^(a+5) /(a+5))−(x^(a+7) /(a+7))....∣_0 ^1 =(1/(a+1))−(1/(a+3))+(1/(a+5))−(1/(a+7))+... now (dI/da)=(1/(a+1))−(1/(a+3))+(1/(a+5))−(1/(a+7))+... ∫dI=∫((1/(a+1))−(1/(a+3))+(1/(a+5))−(1/(a+7))+...)da I(a)=[ln(a+1)−ln(a+3)+ln(a+5)−...]+c I(a)=∫_0 ^1 ((x^a −1)/((1+x^2 )lnx))dx when a=0 I(a)=0 so 0=[ln1−ln3+ln5−ln7...]+c c=−ln1+ln3−ln5+ln7... now I(a)=[ln(a+1)−ln( a+3)+ln(a+5)−...]+δ so answer is put a=3 [ln(4)−ln(6)+ln(8)−ln(10)...]+[ln3−ln5+ln7−ln11..] I=Σ_(r=1) ^∞ (−1)^(r−1) [ln(2+2r)+ln(1+2r)] =Σ_(r=1) ^∞ (−1)^(r−1) [ln2+ln{(1+r)(1+2r)}] pls others pls check...](https://www.tinkutara.com/question/Q52951.png)
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }×\frac{{dx}}{{lnx}} \\ $$$$\frac{{dI}_{} }{{da}}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial{a}}\left(\frac{{x}^{{a}} −\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right)×\frac{{dx}}{{lnx}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} {lnx}}{\mathrm{1}+{x}^{\mathrm{2}} }×\frac{{dx}}{{lnx}} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx}\:\:\:\: \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} \left(\mathrm{1}−{x}^{\mathrm{2}} +{x}^{\mathrm{4}} −{x}^{\mathrm{6}} +…\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} −{x}^{\mathrm{2}+{a}} +{x}^{\mathrm{4}+{a}} −{x}^{\mathrm{6}+{a}} +…{dx} \\ $$$$=\mid\frac{{x}^{{a}+\mathrm{1}} }{{a}+\mathrm{1}}−\frac{{x}^{{a}+\mathrm{3}} }{{a}+\mathrm{3}}−\frac{{x}^{{a}+\mathrm{5}} }{{a}+\mathrm{5}}−\frac{{x}^{{a}+\mathrm{7}} }{{a}+\mathrm{7}}….\mid_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{{a}+\mathrm{1}}−\frac{\mathrm{1}}{{a}+\mathrm{3}}+\frac{\mathrm{1}}{{a}+\mathrm{5}}−\frac{\mathrm{1}}{{a}+\mathrm{7}}+… \\ $$$${now}\:\frac{{dI}}{{da}}=\frac{\mathrm{1}}{{a}+\mathrm{1}}−\frac{\mathrm{1}}{{a}+\mathrm{3}}+\frac{\mathrm{1}}{{a}+\mathrm{5}}−\frac{\mathrm{1}}{{a}+\mathrm{7}}+… \\ $$$$\int{dI}=\int\left(\frac{\mathrm{1}}{{a}+\mathrm{1}}−\frac{\mathrm{1}}{{a}+\mathrm{3}}+\frac{\mathrm{1}}{{a}+\mathrm{5}}−\frac{\mathrm{1}}{{a}+\mathrm{7}}+…\right){da} \\ $$$${I}\left({a}\right)=\left[{ln}\left({a}+\mathrm{1}\right)−{ln}\left({a}+\mathrm{3}\right)+{ln}\left({a}+\mathrm{5}\right)−…\right]+{c} \\ $$$$ \\ $$$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{\left(\mathrm{1}+{x}^{\mathrm{2}} \right){lnx}}{dx}\: \\ $$$${when}\:{a}=\mathrm{0}\:\:{I}\left({a}\right)=\mathrm{0} \\ $$$${so}\:\:\mathrm{0}=\left[{ln}\mathrm{1}−{ln}\mathrm{3}+{ln}\mathrm{5}−{ln}\mathrm{7}…\right]+{c} \\ $$$${c}=−{ln}\mathrm{1}+{ln}\mathrm{3}−{ln}\mathrm{5}+{ln}\mathrm{7}… \\ $$$$\:\: \\ $$$$ \\ $$$$\:{now}\:{I}\left({a}\right)=\left[{ln}\left({a}+\mathrm{1}\right)−{ln}\left(\:{a}+\mathrm{3}\right)+{ln}\left({a}+\mathrm{5}\right)−…\right]+\delta \\ $$$${so}\:{answer}\:{is}\:{put}\:{a}=\mathrm{3} \\ $$$$\left[{ln}\left(\mathrm{4}\right)−{ln}\left(\mathrm{6}\right)+{ln}\left(\mathrm{8}\right)−{ln}\left(\mathrm{10}\right)…\right]+\left[{ln}\mathrm{3}−{ln}\mathrm{5}+{ln}\mathrm{7}−{ln}\mathrm{11}..\right] \\ $$$${I}=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} \:\left[{ln}\left(\mathrm{2}+\mathrm{2}{r}\right)+{ln}\left(\mathrm{1}+\mathrm{2}{r}\right)\right] \\ $$$$=\underset{{r}=\mathrm{1}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{r}−\mathrm{1}} \left[{ln}\mathrm{2}+{ln}\left\{\left(\mathrm{1}+{r}\right)\left(\mathrm{1}+\mathrm{2}{r}\right)\right\}\right] \\ $$$${pls}\:{others}\:{pls}\:{check}… \\ $$
Commented by Tawa1 last updated on 15/Jan/19

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
