Question Number 128373 by BHOOPENDRA last updated on 06/Jan/21
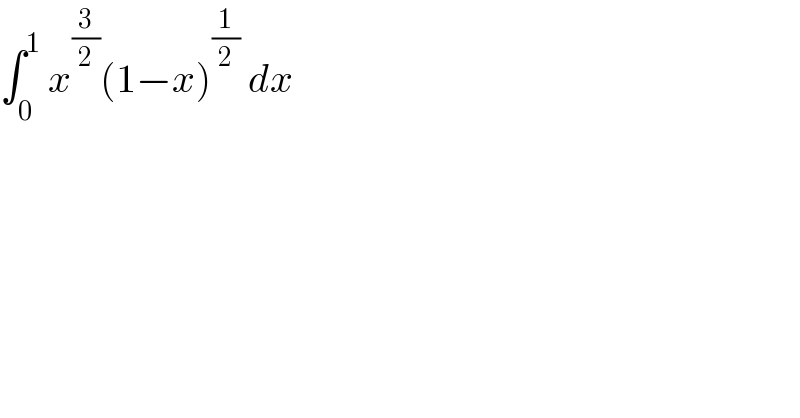
$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} \:{dx} \\ $$
Answered by Dwaipayan Shikari last updated on 06/Jan/21
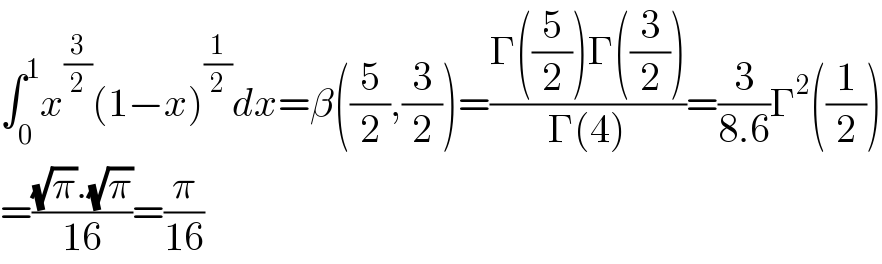
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}−{x}\right)^{\frac{\mathrm{1}}{\mathrm{2}}} {dx}=\beta\left(\frac{\mathrm{5}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)=\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{4}\right)}=\frac{\mathrm{3}}{\mathrm{8}.\mathrm{6}}\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$$=\frac{\sqrt{\pi}.\sqrt{\pi}}{\mathrm{16}}=\frac{\pi}{\mathrm{16}} \\ $$
