0-1-x-3-2-1-x-dx-

Question Number 102169 by bemath last updated on 07/Jul/20

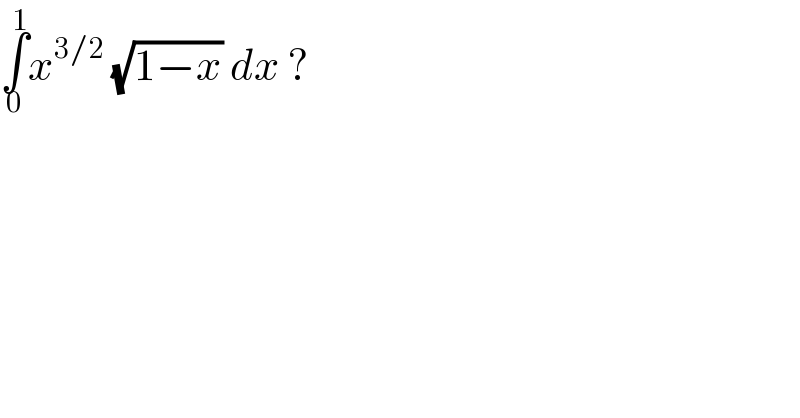
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{x}^{\mathrm{3}/\mathrm{2}} \:\sqrt{\mathrm{1}−{x}}\:{dx}\:? \\ $$

Answered by bemath last updated on 07/Jul/20

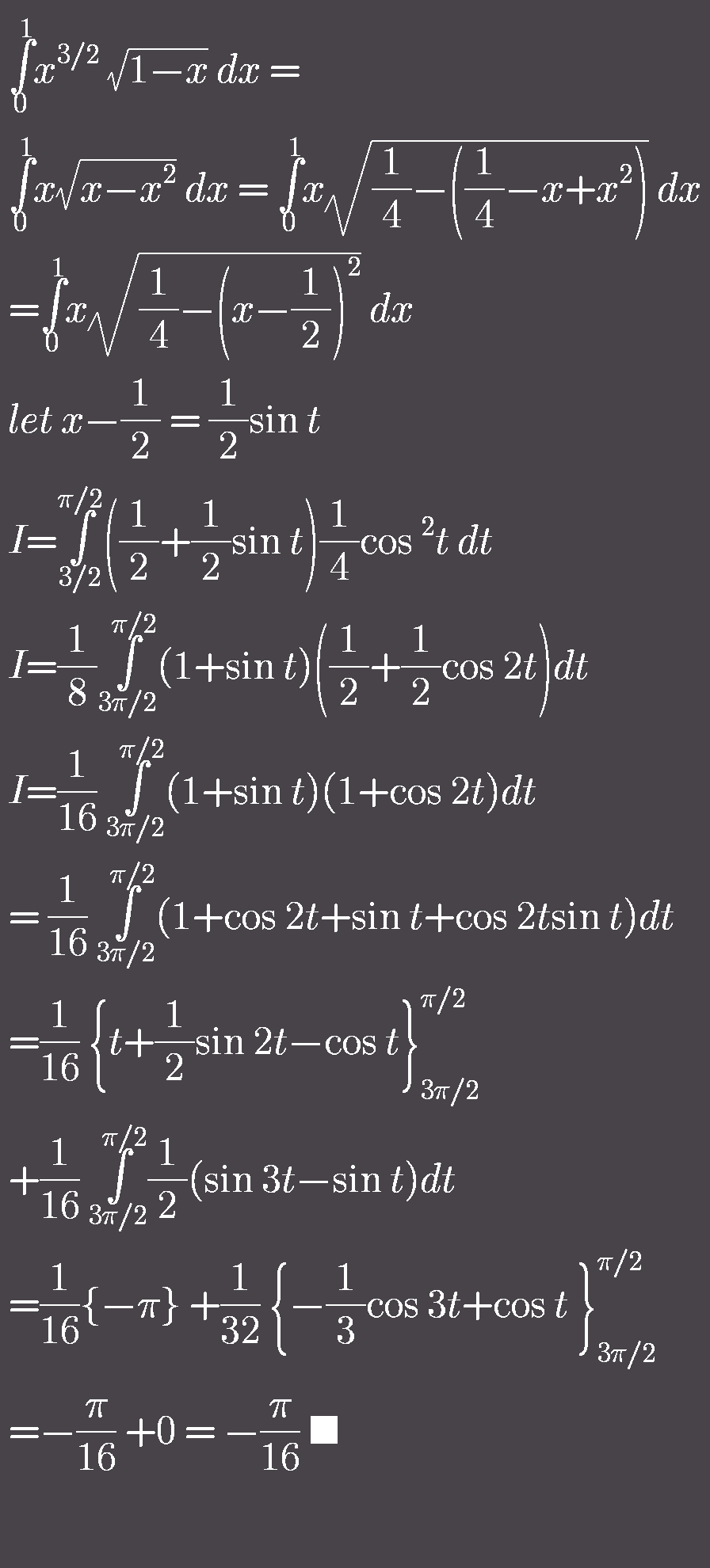
Answered by john santu last updated on 07/Jul/20

I=∫_0 ^1 x^(3/2) (√(1−x)) dx replace 1−x by x I=∫_0 ^1 (1−x)^(3/2) (√x) dx ⇒2I = ∫_0 ^1 ( x^(3/2) (√(1−x)) +(1−x)^(3/2) (√(x )) )dx 2I= ∫_0 ^1 (√x) (√(1−x )) (x+1−x) dx I = (1/2)∫_0 ^1 (√(x−x^2 )) dx I= (1/2)∫_0 ^1 (√((1/4)−((1/4)−x+x^2 ))) dx I=(1/2)∫_0 ^1 (√((1/4)−(x−(1/2))^2 )) dx set x−(1/2) = (1/2)t ⇒I=(1/2)∫_(−1) ^1 (√((1/4)−(1/4)t^2 )) ((1/2)dt) I = (1/8)∫_(−1) ^1 (√(1−t^2 )) dt = (π/(16)) ⊛ [ ∫_(−1) ^1 (√(1−x^2 )) dx = (1/2)π(1)^2 ] the area of a half circle with radius 1 ]

$${I}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{x}^{\mathrm{3}/\mathrm{2}} \:\sqrt{\mathrm{1}−{x}}\:{dx}\: \\ $$$${replace}\:\mathrm{1}−{x}\:{by}\:{x}\: \\ $$$${I}=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{2}} \:\sqrt{{x}}\:{dx}\: \\ $$$$\Rightarrow\mathrm{2}{I}\:=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left(\:{x}^{\mathrm{3}/\mathrm{2}} \sqrt{\mathrm{1}−{x}}\:+\left(\mathrm{1}−{x}\right)^{\mathrm{3}/\mathrm{2}} \sqrt{{x}\:}\:\right){dx} \\ $$$$\mathrm{2}{I}=\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\sqrt{{x}}\:\sqrt{\mathrm{1}−{x}\:}\:\left({x}+\mathrm{1}−{x}\right)\:{dx}\: \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt{{x}−{x}^{\mathrm{2}} }\:{dx}\: \\ $$$${I}=\:\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\left(\frac{\mathrm{1}}{\mathrm{4}}−{x}+{x}^{\mathrm{2}} \right)}\:{dx} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }\:{dx}\: \\ $$$${set}\:{x}−\frac{\mathrm{1}}{\mathrm{2}}\:=\:\frac{\mathrm{1}}{\mathrm{2}}{t}\:\Rightarrow{I}=\frac{\mathrm{1}}{\mathrm{2}}\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{4}}{t}^{\mathrm{2}} }\:\left(\frac{\mathrm{1}}{\mathrm{2}}{dt}\right) \\ $$$${I}\:=\:\frac{\mathrm{1}}{\mathrm{8}}\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{1}−{t}^{\mathrm{2}} }\:{dt}\:=\:\frac{\pi}{\mathrm{16}}\:\circledast \\ $$$$\left[\:\underset{−\mathrm{1}} {\overset{\mathrm{1}} {\int}}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }\:{dx}\:=\:\frac{\mathrm{1}}{\mathrm{2}}\pi\left(\mathrm{1}\right)^{\mathrm{2}} \:\right]\: \\ $$$$\left.{the}\:{area}\:{of}\:{a}\:{half}\:{circle}\:{with}\:{radius}\:\mathrm{1}\:\right] \\ $$

Answered by 1549442205 last updated on 08/Jul/20

Putting (1/x)−1=t^2 ⇒−(1/x^2 )dx=2tdt ⇒x=(1/(1+t^2 )), (√(1−x))=(t/( (√(1+t^2 )))),dx =−((2tdt)/((t^2 +1)^2 )) F=−2∫((1/(1+t^2 )))^(3/2) .(t^2 /((1+t^2 )^2 (√(1+t^2 ))))dt =−2∫((t^2 dt)/((1+t^2 )^4 ))=−2∫(((1+t^2 )−1)/((1+t^2 )^4 ))dt=−2∫(dt/((1+t^2 )^3 ))+2∫(dt/((1+t^2 )^4 )) Applying the current formular: I_n =∫(dt/((1+t^2 )^n ))=(1/2).(t/((1+t^2 )^(n−1) ))+(1/2).((2n−3)/(2n−2)).I_(n−1) we get I_2 =(1/(2(2−1))).(t/((1+t^2 )^(2−1) ))+((2.2−3)/(2.3−2))I_(2−1) =(1/2).(t/(t^2 +1))+(1/2)I_1 =(t/(2(t^2 +1)))+(1/2)∫(dt/(t^2 +1))=(t/(2(t^2 +1)))+(1/2)arctan t+C_1 I_3 =(1/(2(3−1))).(t/((t^2 +1)^(3−1) ))+((2.3−3)/(2.3−2))I_(3−1) = (1/4)(t/((t^2 +1)^2 ))+(3/4)I_2 =(t/(4(t^2 +1)^2 ))+((3t)/(8(t^2 +1)))+(3/8)arctan t I_4 =(1/(2(4−1))). (t/((t^2 +1)^(4−1) ))+((2.4−3)/(2.4−2)).I_3 = =(1/6).(t/((t^2 +1)^3 ))+(5/6).I_3 =(t/(6(t^2 +1)^3 ))+((5t)/(24(t^2 +1)^2 ))+((5t)/(16(t^2 +1)))+(5/(16))arctan t We get F=2(I_4 −I_3 )=(t/(8(t^2 +1)^3 ))−(t/(12(t^2 +1)^2 ))−(t/(8(t^2 +1)))+((arctan t)/8) Hence,∫_0 ^1 x^(3/2) (√(1−x))dx=F(∞)−F(0)=(𝛑/(16))−0=(𝛑/(16))

$$\mathrm{Putting}\:\frac{\mathrm{1}}{\mathrm{x}}−\mathrm{1}=\mathrm{t}^{\mathrm{2}} \Rightarrow−\frac{\mathrm{1}}{\mathrm{x}^{\mathrm{2}} }\mathrm{dx}=\mathrm{2tdt} \\ $$$$\Rightarrow\mathrm{x}=\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} },\:\:\:\:\:\sqrt{\mathrm{1}−\mathrm{x}}=\frac{\mathrm{t}}{\:\sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }},\mathrm{dx}\:=−\frac{\mathrm{2tdt}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\:\mathrm{F}=−\mathrm{2}\int\left(\frac{\mathrm{1}}{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }\right)^{\frac{\mathrm{3}}{\mathrm{2}}} .\frac{\mathrm{t}^{\mathrm{2}} }{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} \sqrt{\mathrm{1}+\mathrm{t}^{\mathrm{2}} }}\mathrm{dt} \\ $$$$=−\mathrm{2}\int\frac{\mathrm{t}^{\mathrm{2}} \mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{4}} }=−\mathrm{2}\int\frac{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)−\mathrm{1}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{4}} }\mathrm{dt}=−\mathrm{2}\int\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{3}} }+\mathrm{2}\int\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{4}} } \\ $$$$\mathrm{Applying}\:\mathrm{the}\:\mathrm{current}\:\mathrm{formular}: \\ $$$$\mathrm{I}_{\mathrm{n}} =\int\frac{\mathrm{dt}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{n}} }=\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{t}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{n}−\mathrm{1}} }+\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{2n}−\mathrm{3}}{\mathrm{2n}−\mathrm{2}}.\mathrm{I}_{\mathrm{n}−\mathrm{1}} \\ $$$$\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{I}_{\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}−\mathrm{1}\right)}.\frac{\mathrm{t}}{\left(\mathrm{1}+\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}−\mathrm{1}} }+\frac{\mathrm{2}.\mathrm{2}−\mathrm{3}}{\mathrm{2}.\mathrm{3}−\mathrm{2}}\mathrm{I}_{\mathrm{2}−\mathrm{1}} =\frac{\mathrm{1}}{\mathrm{2}}.\frac{\mathrm{t}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{I}_{\mathrm{1}} \\ $$$$=\frac{\mathrm{t}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{dt}}{\mathrm{t}^{\mathrm{2}} +\mathrm{1}}=\frac{\mathrm{t}}{\mathrm{2}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\mathrm{t}+\mathrm{C}_{\mathrm{1}} \\ $$$$\mathrm{I}_{\mathrm{3}} =\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{3}−\mathrm{1}\right)}.\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}−\mathrm{1}} }+\frac{\mathrm{2}.\mathrm{3}−\mathrm{3}}{\mathrm{2}.\mathrm{3}−\mathrm{2}}\mathrm{I}_{\mathrm{3}−\mathrm{1}} = \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{3}}{\mathrm{4}}\mathrm{I}_{\mathrm{2}} =\frac{\mathrm{t}}{\mathrm{4}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{3t}}{\mathrm{8}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{3}}{\mathrm{8}}\mathrm{arctan}\:\mathrm{t} \\ $$$$\mathrm{I}_{\mathrm{4}} =\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{4}−\mathrm{1}\right)}.\:\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}−\mathrm{1}} }+\frac{\mathrm{2}.\mathrm{4}−\mathrm{3}}{\mathrm{2}.\mathrm{4}−\mathrm{2}}.\mathrm{I}_{\mathrm{3}} = \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}.\frac{\mathrm{t}}{\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{6}}.\mathrm{I}_{\mathrm{3}} =\frac{\mathrm{t}}{\mathrm{6}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{5t}}{\mathrm{24}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }+\frac{\mathrm{5t}}{\mathrm{16}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{5}}{\mathrm{16}}\mathrm{arctan}\:\mathrm{t} \\ $$$$\mathrm{We}\:\mathrm{get}\:\mathrm{F}=\mathrm{2}\left(\mathrm{I}_{\mathrm{4}} −\mathrm{I}_{\mathrm{3}} \right)=\frac{\mathrm{t}}{\mathrm{8}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }−\frac{\mathrm{t}}{\mathrm{12}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{2}} }−\frac{\mathrm{t}}{\mathrm{8}\left(\mathrm{t}^{\mathrm{2}} +\mathrm{1}\right)}+\frac{\mathrm{arctan}\:\mathrm{t}}{\mathrm{8}} \\ $$$$\boldsymbol{\mathrm{Hence}},\int_{\mathrm{0}} ^{\mathrm{1}} \boldsymbol{\mathrm{x}}^{\frac{\mathrm{3}}{\mathrm{2}}} \sqrt{\mathrm{1}−\boldsymbol{\mathrm{x}}}\boldsymbol{\mathrm{dx}}=\boldsymbol{\mathrm{F}}\left(\infty\right)−\boldsymbol{\mathrm{F}}\left(\mathrm{0}\right)=\frac{\boldsymbol{\pi}}{\mathrm{16}}−\mathrm{0}=\frac{\boldsymbol{\pi}}{\mathrm{16}} \\ $$

Commented by mathmax by abdo last updated on 07/Jul/20

the functin x→x^(3/2) (√(1−x))is ≥0 on [0,1] ⇒∫_0 ^1 x^(3/2) (√(1−x))dx ≥0 ...!

$$\mathrm{the}\:\mathrm{functin}\:\mathrm{x}\rightarrow\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \sqrt{\mathrm{1}−\mathrm{x}}\mathrm{is}\:\geqslant\mathrm{0}\:\mathrm{on}\:\left[\mathrm{0},\mathrm{1}\right]\:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \sqrt{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:\geqslant\mathrm{0}\:…! \\ $$

Commented by 1549442205 last updated on 08/Jul/20

Thank you sir.I shall check again later. Now I corrected

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{sir}.\mathrm{I}\:\mathrm{shall}\:\mathrm{check}\:\mathrm{again}\:\mathrm{later}. \\ $$$$\mathrm{Now}\:\mathrm{I}\:\mathrm{corrected} \\ $$

Answered by mathmax by abdo last updated on 07/Jul/20

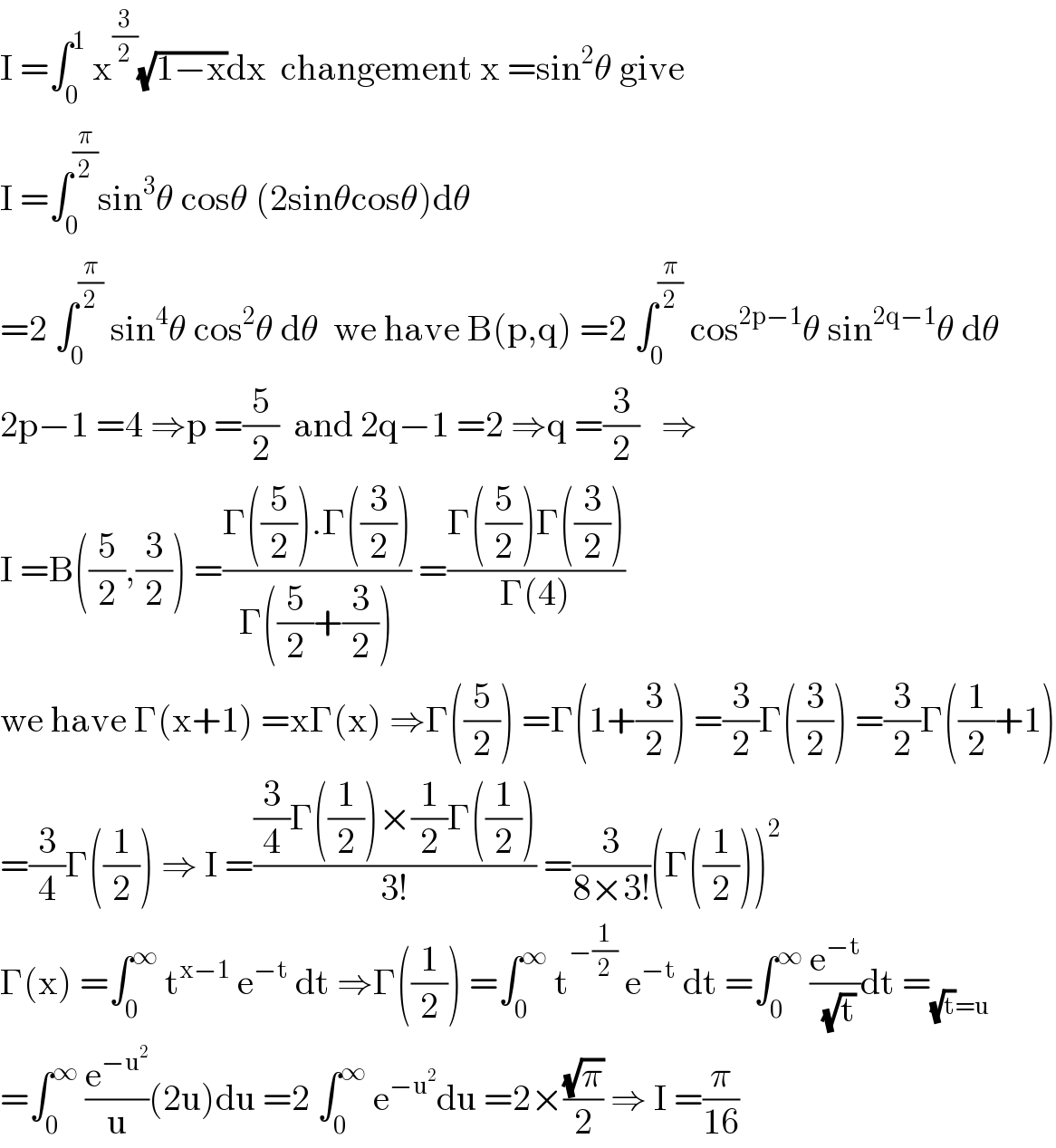
I =∫_0 ^1 x^(3/2) (√(1−x))dx changement x =sin^2 θ give I =∫_0 ^(π/2) sin^3 θ cosθ (2sinθcosθ)dθ =2 ∫_0 ^(π/2) sin^4 θ cos^2 θ dθ we have B(p,q) =2 ∫_0 ^(π/2) cos^(2p−1) θ sin^(2q−1) θ dθ 2p−1 =4 ⇒p =(5/2) and 2q−1 =2 ⇒q =(3/2) ⇒ I =B((5/2),(3/2)) =((Γ((5/2)).Γ((3/2)))/(Γ((5/2)+(3/2)))) =((Γ((5/2))Γ((3/2)))/(Γ(4))) we have Γ(x+1) =xΓ(x) ⇒Γ((5/2)) =Γ(1+(3/2)) =(3/2)Γ((3/2)) =(3/2)Γ((1/2)+1) =(3/4)Γ((1/2)) ⇒ I =(((3/4)Γ((1/2))×(1/2)Γ((1/2)))/(3!)) =(3/(8×3!))(Γ((1/2)))^2 Γ(x) =∫_0 ^∞ t^(x−1) e^(−t) dt ⇒Γ((1/2)) =∫_0 ^∞ t^(−(1/2)) e^(−t) dt =∫_0 ^∞ (e^(−t) /( (√t)))dt =_((√t)=u) =∫_0 ^∞ (e^(−u^2 ) /u)(2u)du =2 ∫_0 ^∞ e^(−u^2 ) du =2×((√π)/2) ⇒ I =(π/(16))

$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\mathrm{x}^{\frac{\mathrm{3}}{\mathrm{2}}} \sqrt{\mathrm{1}−\mathrm{x}}\mathrm{dx}\:\:\mathrm{changement}\:\mathrm{x}\:=\mathrm{sin}^{\mathrm{2}} \theta\:\mathrm{give} \\ $$$$\mathrm{I}\:=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{sin}^{\mathrm{3}} \theta\:\mathrm{cos}\theta\:\left(\mathrm{2sin}\theta\mathrm{cos}\theta\right)\mathrm{d}\theta \\ $$$$=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{sin}^{\mathrm{4}} \theta\:\mathrm{cos}^{\mathrm{2}} \theta\:\mathrm{d}\theta\:\:\mathrm{we}\:\mathrm{have}\:\mathrm{B}\left(\mathrm{p},\mathrm{q}\right)\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{cos}^{\mathrm{2p}−\mathrm{1}} \theta\:\mathrm{sin}^{\mathrm{2q}−\mathrm{1}} \theta\:\mathrm{d}\theta \\ $$$$\mathrm{2p}−\mathrm{1}\:=\mathrm{4}\:\Rightarrow\mathrm{p}\:=\frac{\mathrm{5}}{\mathrm{2}}\:\:\mathrm{and}\:\mathrm{2q}−\mathrm{1}\:=\mathrm{2}\:\Rightarrow\mathrm{q}\:=\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\Rightarrow \\ $$$$\mathrm{I}\:=\mathrm{B}\left(\frac{\mathrm{5}}{\mathrm{2}},\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right).\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}}\right)}\:=\frac{\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)}{\Gamma\left(\mathrm{4}\right)} \\ $$$$\mathrm{we}\:\mathrm{have}\:\Gamma\left(\mathrm{x}+\mathrm{1}\right)\:=\mathrm{x}\Gamma\left(\mathrm{x}\right)\:\Rightarrow\Gamma\left(\frac{\mathrm{5}}{\mathrm{2}}\right)\:=\Gamma\left(\mathrm{1}+\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\mathrm{3}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{3}}{\mathrm{2}}\right)\:=\frac{\mathrm{3}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right) \\ $$$$=\frac{\mathrm{3}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:\Rightarrow\:\mathrm{I}\:=\frac{\frac{\mathrm{3}}{\mathrm{4}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)×\frac{\mathrm{1}}{\mathrm{2}}\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)}{\mathrm{3}!}\:=\frac{\mathrm{3}}{\mathrm{8}×\mathrm{3}!}\left(\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\right)^{\mathrm{2}} \\ $$$$\Gamma\left(\mathrm{x}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{\mathrm{x}−\mathrm{1}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:\Rightarrow\Gamma\left(\frac{\mathrm{1}}{\mathrm{2}}\right)\:=\int_{\mathrm{0}} ^{\infty} \:\mathrm{t}^{−\frac{\mathrm{1}}{\mathrm{2}}} \:\mathrm{e}^{−\mathrm{t}} \:\mathrm{dt}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{t}} }{\:\sqrt{\mathrm{t}}}\mathrm{dt}\:=_{\sqrt{\mathrm{t}}=\mathrm{u}} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \:\frac{\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } }{\mathrm{u}}\left(\mathrm{2u}\right)\mathrm{du}\:=\mathrm{2}\:\int_{\mathrm{0}} ^{\infty} \:\mathrm{e}^{−\mathrm{u}^{\mathrm{2}} } \mathrm{du}\:=\mathrm{2}×\frac{\sqrt{\pi}}{\mathrm{2}}\:\Rightarrow\:\mathrm{I}\:=\frac{\pi}{\mathrm{16}} \\ $$

Answered by Dwaipayan Shikari last updated on 07/Jul/20

∫_0 ^1 (1−x)^(3/2) (√x)dx=∫_0 ^1 (((x−x^2 )^(3/2) )/x)=∫_0 ^1 (1−x)(√(x−x^2 ))=(1/2)∫_0 ^1 (1+1−2x)(√(x−x^2 )) (1/2)∫_0 ^1 (√(x−x^2 ))+(1/2)∫_0 ^1 (1−2x)(√(x−x^2 ))dx=(1/2)∫_0 ^1 (√((1/4)−(x−(1/2))^2 ))+(1/3)(0) (1/2)∫_0 ^1 (√(((1/2))^2 −(x−(1/2))^2 ))dx=[((x−(1/2))/4)(√(x−x^2 ))]_0 ^1 −(1/(16))sin^(−1) [((x−(1/2))/(1/2))]_0 ^1 =0−(π/(32))+((3π)/(32))=(π/(16)) {Note: ∫_0 ^1 (1−2x)(√(x−x^2 ))=0

$$\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \sqrt{{x}}{dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left({x}−{x}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{{x}}=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−{x}\right)\sqrt{{x}−{x}^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}+\mathrm{1}−\mathrm{2}{x}\right)\sqrt{{x}−{x}^{\mathrm{2}} } \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{{x}−{x}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{2}{x}\right)\sqrt{{x}−{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\frac{\mathrm{1}}{\mathrm{4}}−\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{3}}\left(\mathrm{0}\right) \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\mathrm{1}} \sqrt{\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} −\left({x}−\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }{dx}=\left[\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{4}}\sqrt{{x}−{x}^{\mathrm{2}} }\right]_{\mathrm{0}} ^{\mathrm{1}} −\frac{\mathrm{1}}{\mathrm{16}}{sin}^{−\mathrm{1}} \left[\frac{{x}−\frac{\mathrm{1}}{\mathrm{2}}}{\frac{\mathrm{1}}{\mathrm{2}}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\mathrm{0}−\frac{\pi}{\mathrm{32}}+\frac{\mathrm{3}\pi}{\mathrm{32}}=\frac{\pi}{\mathrm{16}}\:\:\:\:\:\:\:\:\:\:\:\left\{{Note}:\:\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\mathrm{2}{x}\right)\sqrt{{x}−{x}^{\mathrm{2}} }=\mathrm{0}\right. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply