Question Number 166307 by ArielVyny last updated on 18/Feb/22
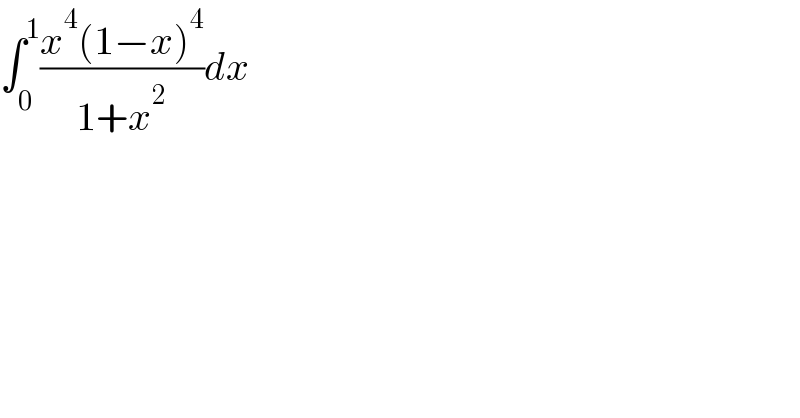
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{4}} \left(\mathrm{1}−{x}\right)^{\mathrm{4}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$
Answered by MJS_new last updated on 18/Feb/22
![∫_0 ^1 ((x^4 (1−x)^4 )/(x^2 +1))dx= =∫_0 ^1 (x^6 −4x^5 +5x^4 −4x^2 +4−(4/(x^2 +1)))dx= =[(x^7 /7)−((2x^6 )/3)+x^5 −((4x^3 )/3)+4x−4arctan x]_0 ^1 = =((22)/7)−π](https://www.tinkutara.com/question/Q166316.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\frac{{x}^{\mathrm{4}} \left(\mathrm{1}−{x}\right)^{\mathrm{4}} }{{x}^{\mathrm{2}} +\mathrm{1}}{dx}= \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\left({x}^{\mathrm{6}} −\mathrm{4}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{4}} −\mathrm{4}{x}^{\mathrm{2}} +\mathrm{4}−\frac{\mathrm{4}}{{x}^{\mathrm{2}} +\mathrm{1}}\right){dx}= \\ $$$$=\left[\frac{{x}^{\mathrm{7}} }{\mathrm{7}}−\frac{\mathrm{2}{x}^{\mathrm{6}} }{\mathrm{3}}+{x}^{\mathrm{5}} −\frac{\mathrm{4}{x}^{\mathrm{3}} }{\mathrm{3}}+\mathrm{4}{x}−\mathrm{4arctan}\:{x}\right]_{\mathrm{0}} ^{\mathrm{1}} = \\ $$$$=\frac{\mathrm{22}}{\mathrm{7}}−\pi \\ $$
Commented by ArielVyny last updated on 19/Feb/22

$${exact}\:{sir}\:{thank} \\ $$
