Question Number 145378 by mnjuly1970 last updated on 04/Jul/21
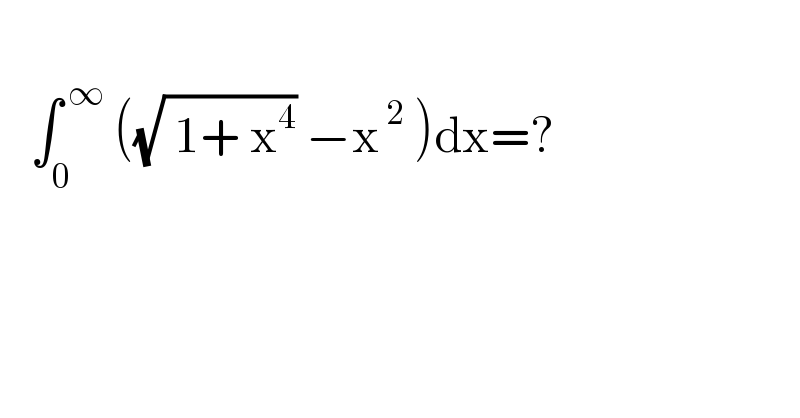
$$ \\ $$$$\:\:\:\int_{\mathrm{0}} ^{\:\infty} \:\left(\sqrt{\:\mathrm{1}+\:\mathrm{x}^{\mathrm{4}} }\:−\mathrm{x}^{\:\mathrm{2}} \:\right)\mathrm{dx}=? \\ $$
Answered by qaz last updated on 05/Jul/21
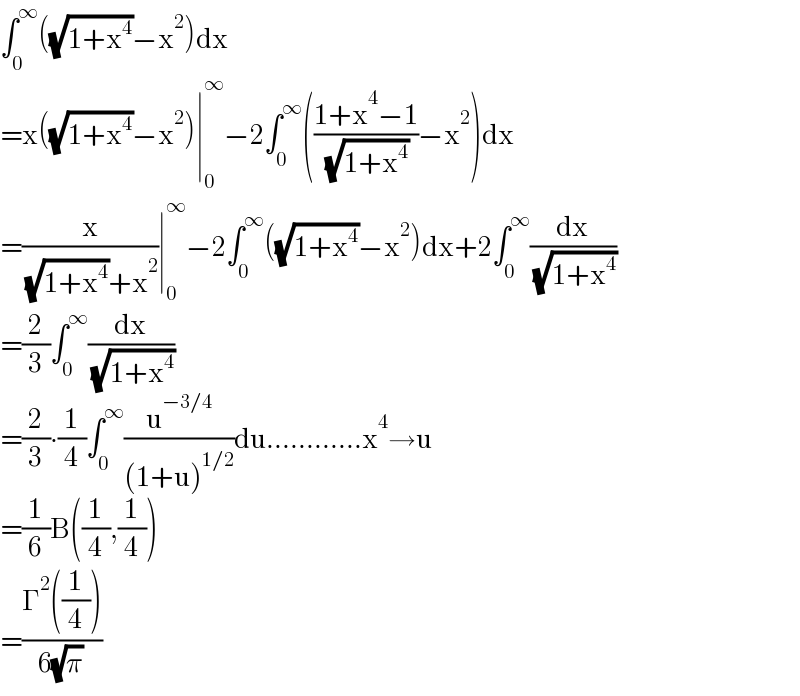
$$\int_{\mathrm{0}} ^{\infty} \left(\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\mathrm{x}\left(\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }−\mathrm{x}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\infty} −\mathrm{2}\int_{\mathrm{0}} ^{\infty} \left(\frac{\mathrm{1}+\mathrm{x}^{\mathrm{4}} −\mathrm{1}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }}−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx} \\ $$$$=\frac{\mathrm{x}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }+\mathrm{x}^{\mathrm{2}} }\mid_{\mathrm{0}} ^{\infty} −\mathrm{2}\int_{\mathrm{0}} ^{\infty} \left(\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }−\mathrm{x}^{\mathrm{2}} \right)\mathrm{dx}+\mathrm{2}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{dx}}{\:\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{4}} }} \\ $$$$=\frac{\mathrm{2}}{\mathrm{3}}\centerdot\frac{\mathrm{1}}{\mathrm{4}}\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{u}^{−\mathrm{3}/\mathrm{4}} }{\left(\mathrm{1}+\mathrm{u}\right)^{\mathrm{1}/\mathrm{2}} }\mathrm{du}…………\mathrm{x}^{\mathrm{4}} \rightarrow\mathrm{u} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\mathrm{B}\left(\frac{\mathrm{1}}{\mathrm{4}},\frac{\mathrm{1}}{\mathrm{4}}\right) \\ $$$$=\frac{\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{4}}\right)}{\mathrm{6}\sqrt{\pi}} \\ $$
Commented by mnjuly1970 last updated on 05/Jul/21
$$\:\:{very}\:{nice}\:{mr}\:{qaz} \\ $$$${thx}\:{alot}… \\ $$
