Question Number 121225 by benjo_mathlover last updated on 06/Nov/20
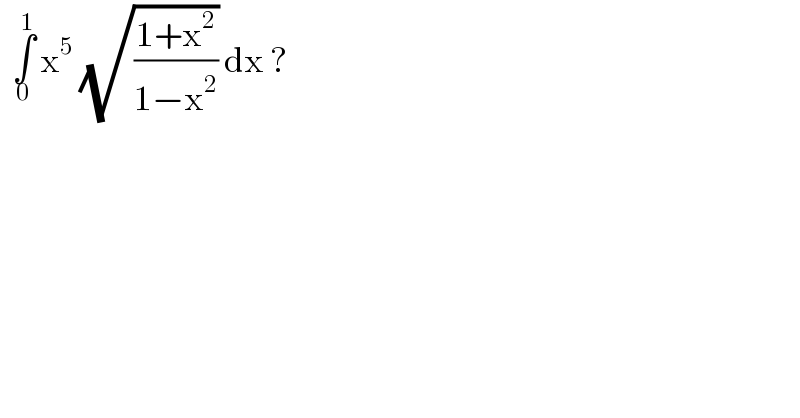
$$\:\:\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\mathrm{x}^{\mathrm{5}} \:\sqrt{\frac{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\mathrm{dx}\:? \\ $$
Answered by liberty last updated on 06/Nov/20
![let (√(1−x^2 )) = t → { ((x^2 =1−t^2 )),((xdx=−tdt)) :} Λ=∫_1 ^0 ((x^4 (√(1+x^2 )) (x dx))/( (√(1−x^2 )))) Λ=∫_0 ^1 (((1−t^2 )^2 (√(2−t^2 )))/t)(t dt ) Λ=∫_0 ^1 (1−t^2 )^2 (√(2−t^2 )) dt let t = (√2) sin r Λ=∫ (1−2sin^2 r)^2 2 cos^2 r dr Λ=∫(cos^2 2r)(1+cos 2r) dr Λ=∫[((1/2)+(1/2)cos 4r)+(((cos 6r+3cos 2r)/4))]dr Λ=(1/2)r+(1/8)sin 4r+(1/(24))sin 6r+(3/8)sin 2r](https://www.tinkutara.com/question/Q121228.png)
$$\:\mathrm{let}\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }\:=\:\mathrm{t}\:\rightarrow\begin{cases}{\mathrm{x}^{\mathrm{2}} =\mathrm{1}−\mathrm{t}^{\mathrm{2}} }\\{\mathrm{xdx}=−\mathrm{tdt}}\end{cases} \\ $$$$\Lambda=\underset{\mathrm{1}} {\overset{\mathrm{0}} {\int}}\:\:\frac{\mathrm{x}^{\mathrm{4}} \sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }\:\left(\mathrm{x}\:\mathrm{dx}\right)}{\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }} \\ $$$$\Lambda=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} \sqrt{\mathrm{2}−\mathrm{t}^{\mathrm{2}} }}{\mathrm{t}}\left(\mathrm{t}\:\mathrm{dt}\:\right) \\ $$$$\Lambda=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\left(\mathrm{1}−\mathrm{t}^{\mathrm{2}} \right)^{\mathrm{2}} \sqrt{\mathrm{2}−\mathrm{t}^{\mathrm{2}} }\:\mathrm{dt} \\ $$$$\mathrm{let}\:\mathrm{t}\:=\:\sqrt{\mathrm{2}}\:\mathrm{sin}\:\mathrm{r}\: \\ $$$$\Lambda=\int\:\left(\mathrm{1}−\mathrm{2sin}\:^{\mathrm{2}} \mathrm{r}\right)^{\mathrm{2}} \:\mathrm{2}\:\mathrm{cos}\:^{\mathrm{2}} \mathrm{r}\:\mathrm{dr} \\ $$$$\Lambda=\int\left(\mathrm{cos}^{\mathrm{2}} \:\mathrm{2r}\right)\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2r}\right)\:\mathrm{dr} \\ $$$$\Lambda=\int\left[\left(\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{cos}\:\mathrm{4r}\right)+\left(\frac{\mathrm{cos}\:\mathrm{6r}+\mathrm{3cos}\:\mathrm{2r}}{\mathrm{4}}\right)\right]\mathrm{dr} \\ $$$$\Lambda=\frac{\mathrm{1}}{\mathrm{2}}\mathrm{r}+\frac{\mathrm{1}}{\mathrm{8}}\mathrm{sin}\:\mathrm{4r}+\frac{\mathrm{1}}{\mathrm{24}}\mathrm{sin}\:\mathrm{6r}+\frac{\mathrm{3}}{\mathrm{8}}\mathrm{sin}\:\mathrm{2r}\: \\ $$$$ \\ $$
Answered by MJS_new last updated on 06/Nov/20
![∫x^5 (√((1+x^2 )/(1−x^2 )))dx= [t=(√((1+x^2 )/(1−x^2 ))) → dx=((√((1+x^2 )(1−x^2 )^3 ))/(2x))dt] =2∫((t^2 (t^2 −1)^2 )/((t^2 +1)^4 ))dt= [Ostrogradski′s Method] =−((t(9t^4 +4t^2 +3))/(6(t^2 +1)^3 ))+(1/2)∫(dt/(t^2 +1))= −((t(9t^4 +4t^2 +3))/(6(t^2 +1)^3 ))+(1/2)arctan t = =−(((2x^4 +3x^2 +4)(√(1−x^4 )))/(12))+(1/2)arctan ((√(1+x^2 ))/( (√(1−x^2 )))) = =−(((2x^4 +3x^2 +4)(√(1−x^4 )))/(12))+(1/2)arcsin ((√(2(1+x^2 )))/2) +C ⇒ ∫_0 ^1 x^5 (√((1+x^2 )/(1−x^2 )))dx=(π/8)+(1/3)](https://www.tinkutara.com/question/Q121245.png)
$$\int{x}^{\mathrm{5}} \sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}\:\rightarrow\:{dx}=\frac{\sqrt{\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{3}} }}{\mathrm{2}{x}}{dt}\right] \\ $$$$=\mathrm{2}\int\frac{{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} }{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{4}} }{dt}= \\ $$$$\:\:\:\:\:\left[\mathrm{Ostrogradski}'\mathrm{s}\:\mathrm{Method}\right] \\ $$$$=−\frac{{t}\left(\mathrm{9}{t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{6}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{dt}}{{t}^{\mathrm{2}} +\mathrm{1}}= \\ $$$$−\frac{{t}\left(\mathrm{9}{t}^{\mathrm{4}} +\mathrm{4}{t}^{\mathrm{2}} +\mathrm{3}\right)}{\mathrm{6}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\mathrm{3}} }+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:{t}\:= \\ $$$$=−\frac{\left(\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arctan}\:\frac{\sqrt{\mathrm{1}+{x}^{\mathrm{2}} }}{\:\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}\:= \\ $$$$=−\frac{\left(\mathrm{2}{x}^{\mathrm{4}} +\mathrm{3}{x}^{\mathrm{2}} +\mathrm{4}\right)\sqrt{\mathrm{1}−{x}^{\mathrm{4}} }}{\mathrm{12}}+\frac{\mathrm{1}}{\mathrm{2}}\mathrm{arcsin}\:\frac{\sqrt{\mathrm{2}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}}{\mathrm{2}}\:+{C} \\ $$$$\Rightarrow \\ $$$$\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{x}^{\mathrm{5}} \sqrt{\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }}{dx}=\frac{\pi}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{3}} \\ $$
Commented by liberty last updated on 06/Nov/20
$$\mathrm{dasyatt}….\mathrm{great} \\ $$
Commented by MJS_new last updated on 06/Nov/20

$$\mathrm{thank}\:\mathrm{you}! \\ $$
