Question Number 103871 by Dwaipayan Shikari last updated on 17/Jul/20
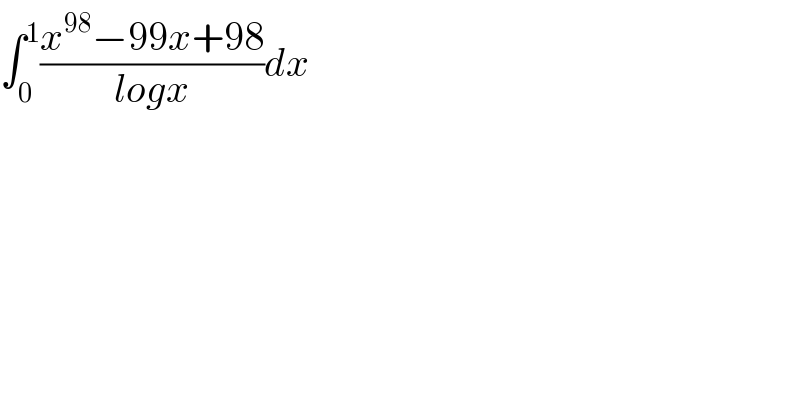
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{98}} −\mathrm{99}{x}+\mathrm{98}}{{logx}}{dx} \\ $$
Commented by Dwaipayan Shikari last updated on 18/Jul/20
![I(a)=∫_0 ^1 ((x^a −1)/(logx)) I^′ (a)=∫_0 ^1 (∂/∂a)(((x^a −1)/(logx)))=∫_0 ^1 ((x^a logx)/(logx))=∫_0 ^1 x^a =[(x^(a+1) /(a+1))]_0 ^1 =(1/(a+1)) ∫I^( ′) (a)=∫(1/(a+1)) I(a)=log(a+1)+C=∫((x^a −1)/(logx)) So , ∫_0 ^1 ((x^(98) −1)/(logx))−99∫_0 ^1 ((x−1)/(logx))=log99−99log2](https://www.tinkutara.com/question/Q103890.png)
$${I}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} −\mathrm{1}}{{logx}} \\ $$$${I}^{'} \left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\partial}{\partial{a}}\left(\frac{{x}^{{a}} −\mathrm{1}}{{logx}}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{a}} {logx}}{{logx}}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} =\left[\frac{{x}^{{a}+\mathrm{1}} }{{a}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$$\int{I}^{\:'} \left({a}\right)=\int\frac{\mathrm{1}}{{a}+\mathrm{1}} \\ $$$${I}\left({a}\right)={log}\left({a}+\mathrm{1}\right)+{C}=\int\frac{{x}^{{a}} −\mathrm{1}}{{logx}} \\ $$$${So}\:, \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{98}} −\mathrm{1}}{{logx}}−\mathrm{99}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}−\mathrm{1}}{{logx}}={log}\mathrm{99}−\mathrm{99}{log}\mathrm{2} \\ $$$$ \\ $$
Commented by Dwaipayan Shikari last updated on 18/Jul/20
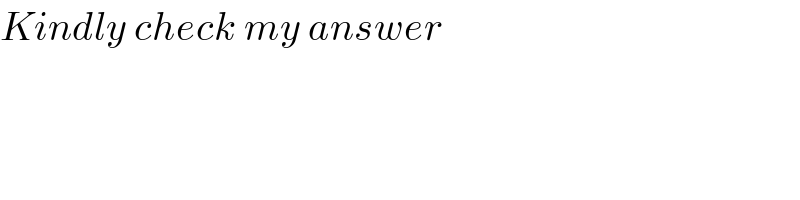
$${Kindly}\:{check}\:{my}\:{answer} \\ $$
Answered by Ar Brandon last updated on 17/Jul/20
![Let x=e^u ⇒dx=e^u du ⇒I=∫_∞ ^0 ((e^(99u) −99e^(2u) +98e^u )/u)du =−∫_0 ^∞ {Σ_(k=0) ^∞ ((99^k u^(k−1) )/(k!))−99Σ_(k=0) ^∞ ((2^k u^(k−1) )/(k!))+98Σ_(k=0) ^∞ (u^(k−1) /(k!))}du =−[Σ_(k=0) ^∞ ((99^k u^k )/(k(k!)))−99Σ_(k=0) ^∞ ((2^k u^k )/(k(k!)))+98Σ_(k=0) ^∞ (u^k /(k(k!)))]_0 ^∞](https://www.tinkutara.com/question/Q103873.png)
$$\mathrm{Let}\:\mathrm{x}=\mathrm{e}^{\mathrm{u}} \Rightarrow\mathrm{dx}=\mathrm{e}^{\mathrm{u}} \mathrm{du} \\ $$$$\Rightarrow\mathcal{I}=\int_{\infty} ^{\mathrm{0}} \frac{\mathrm{e}^{\mathrm{99u}} −\mathrm{99e}^{\mathrm{2u}} +\mathrm{98e}^{\mathrm{u}} }{\mathrm{u}}\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\:=−\int_{\mathrm{0}} ^{\infty} \left\{\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{99}^{\mathrm{k}} \mathrm{u}^{\mathrm{k}−\mathrm{1}} }{\mathrm{k}!}−\mathrm{99}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{\mathrm{k}} \mathrm{u}^{\mathrm{k}−\mathrm{1}} }{\mathrm{k}!}+\mathrm{98}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{u}^{\mathrm{k}−\mathrm{1}} }{\mathrm{k}!}\right\}\mathrm{du} \\ $$$$\:\:\:\:\:\:\:\:=−\left[\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{99}^{\mathrm{k}} \mathrm{u}^{\mathrm{k}} }{\mathrm{k}\left(\mathrm{k}!\right)}−\mathrm{99}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{2}^{\mathrm{k}} \mathrm{u}^{\mathrm{k}} }{\mathrm{k}\left(\mathrm{k}!\right)}+\mathrm{98}\underset{\mathrm{k}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{u}^{\mathrm{k}} }{\mathrm{k}\left(\mathrm{k}!\right)}\right]_{\mathrm{0}} ^{\infty} \\ $$
