Menu Close

0-1-x-ln-1-x-2-dx-ln-27-16-

Tinku Tara 0 Comments
Pin




Question Number 162893 by mnjuly1970 last updated on 02/Jan/22
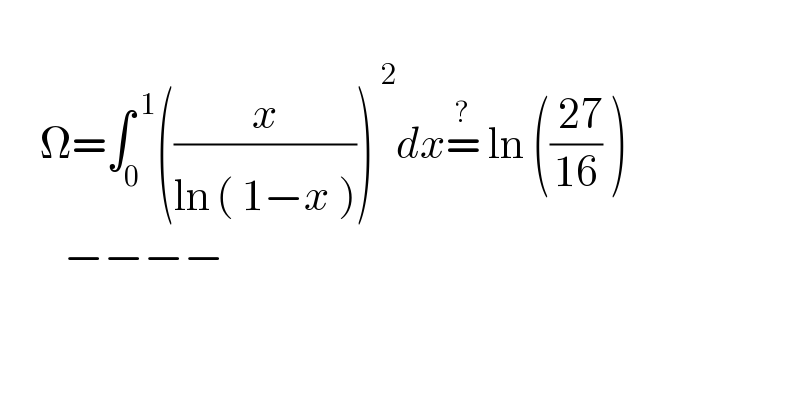
Ω=∫_0 ^( 1) ((( x^ )/(ln^ ( 1−x ))))^( 2) dx=^? ln ((( 27)/(16)) ) −−−−
$$ \\ $$$$\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \left(\frac{\:{x}^{\:} }{\mathrm{ln}^{\:} \left(\:\mathrm{1}−{x}\:\right)}\right)^{\:\mathrm{2}} {dx}\overset{?} {=}\:\mathrm{ln}\:\left(\frac{\:\mathrm{27}}{\mathrm{16}}\:\right) \\ $$$$\:\:\:\:\:\:\:\:−−−− \\ $$$$ \\ $$
Answered by Ar Brandon last updated on 02/Jan/22
Ω=∫_0 ^1 ((x/(ln(1−x))))^2 dx=∫_0 ^1 (((1−x)^2 )/(ln^2 x))dx f(α)=∫_0 ^1 ((x^α (1−x)^2 )/(ln^2 x))dx⇒f^((2)) (α)=∫_0 ^1 x^α (1−x)^2 dx =β(α+1, 3)=((2Γ(α+1))/(Γ(α+4)))=(2/((α+3)(α+2)(α+1))) =(1/(α+3))−(2/(α+2))+(1/(α+1)) ⇒ f^((1)) (α)=ln(α+3)−2ln(α+2)+ln(α+1) f(α)=(α+3)[ln(α+3)−1]−2(α+2)[ln(α+2)−1]+(α+1)[ln(α+1)−1] f(0)=∫_0 ^1 (((1−x)^2 )/(ln^2 x))dx=3(ln3−1)−4(ln2−1)−1 Ω=∫_0 ^1 ((x/(ln(1−x))))^2 dx=ln(((27)/(16)))
$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{x}}{\mathrm{ln}\left(\mathrm{1}−{x}\right)}\right)^{\mathrm{2}} {dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{ln}^{\mathrm{2}} {x}}{dx} \\ $$$${f}\left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\alpha} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{ln}^{\mathrm{2}} {x}}{dx}\Rightarrow{f}^{\left(\mathrm{2}\right)} \left(\alpha\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\alpha} \left(\mathrm{1}−{x}\right)^{\mathrm{2}} {dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\beta\left(\alpha+\mathrm{1},\:\mathrm{3}\right)=\frac{\mathrm{2}\Gamma\left(\alpha+\mathrm{1}\right)}{\Gamma\left(\alpha+\mathrm{4}\right)}=\frac{\mathrm{2}}{\left(\alpha+\mathrm{3}\right)\left(\alpha+\mathrm{2}\right)\left(\alpha+\mathrm{1}\right)} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{1}}{\alpha+\mathrm{3}}−\frac{\mathrm{2}}{\alpha+\mathrm{2}}+\frac{\mathrm{1}}{\alpha+\mathrm{1}}\:\Rightarrow\:{f}^{\left(\mathrm{1}\right)} \left(\alpha\right)=\mathrm{ln}\left(\alpha+\mathrm{3}\right)−\mathrm{2ln}\left(\alpha+\mathrm{2}\right)+\mathrm{ln}\left(\alpha+\mathrm{1}\right) \\ $$$${f}\left(\alpha\right)=\left(\alpha+\mathrm{3}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{3}\right)−\mathrm{1}\right]−\mathrm{2}\left(\alpha+\mathrm{2}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{2}\right)−\mathrm{1}\right]+\left(\alpha+\mathrm{1}\right)\left[\mathrm{ln}\left(\alpha+\mathrm{1}\right)−\mathrm{1}\right] \\ $$$${f}\left(\mathrm{0}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }{\mathrm{ln}^{\mathrm{2}} {x}}{dx}=\mathrm{3}\left(\mathrm{ln3}−\mathrm{1}\right)−\mathrm{4}\left(\mathrm{ln2}−\mathrm{1}\right)−\mathrm{1} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \left(\frac{{x}}{\mathrm{ln}\left(\mathrm{1}−{x}\right)}\right)^{\mathrm{2}} {dx}=\mathrm{ln}\left(\frac{\mathrm{27}}{\mathrm{16}}\right) \\ $$
Commented by Lordose last updated on 02/Jan/22
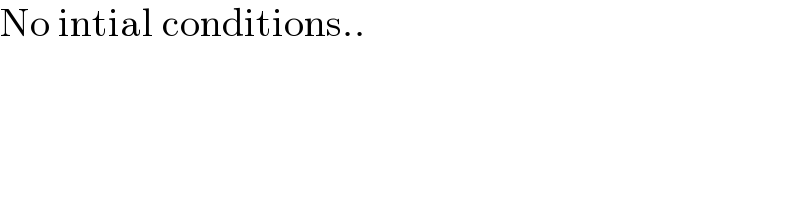
No intial conditions..
$$\mathrm{No}\:\mathrm{intial}\:\mathrm{conditions}.. \\ $$
Commented by Ar Brandon last updated on 02/Jan/22
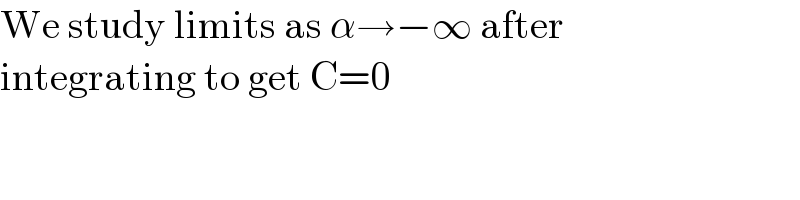
We study limits as α→−∞ after integrating to get C=0
$$\mathrm{We}\:\mathrm{study}\:\mathrm{limits}\:\mathrm{as}\:\alpha\rightarrow−\infty\:\mathrm{after}\: \\ $$$$\mathrm{integrating}\:\mathrm{to}\:\mathrm{get}\:\mathrm{C}=\mathrm{0} \\ $$
Commented by mnjuly1970 last updated on 02/Jan/22
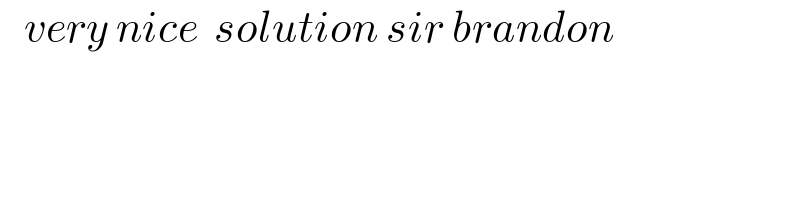
very nice solution sir brandon
$$\:\:\:{very}\:{nice}\:\:{solution}\:{sir}\:{brandon} \\ $$
Answered by Lordose last updated on 02/Jan/22
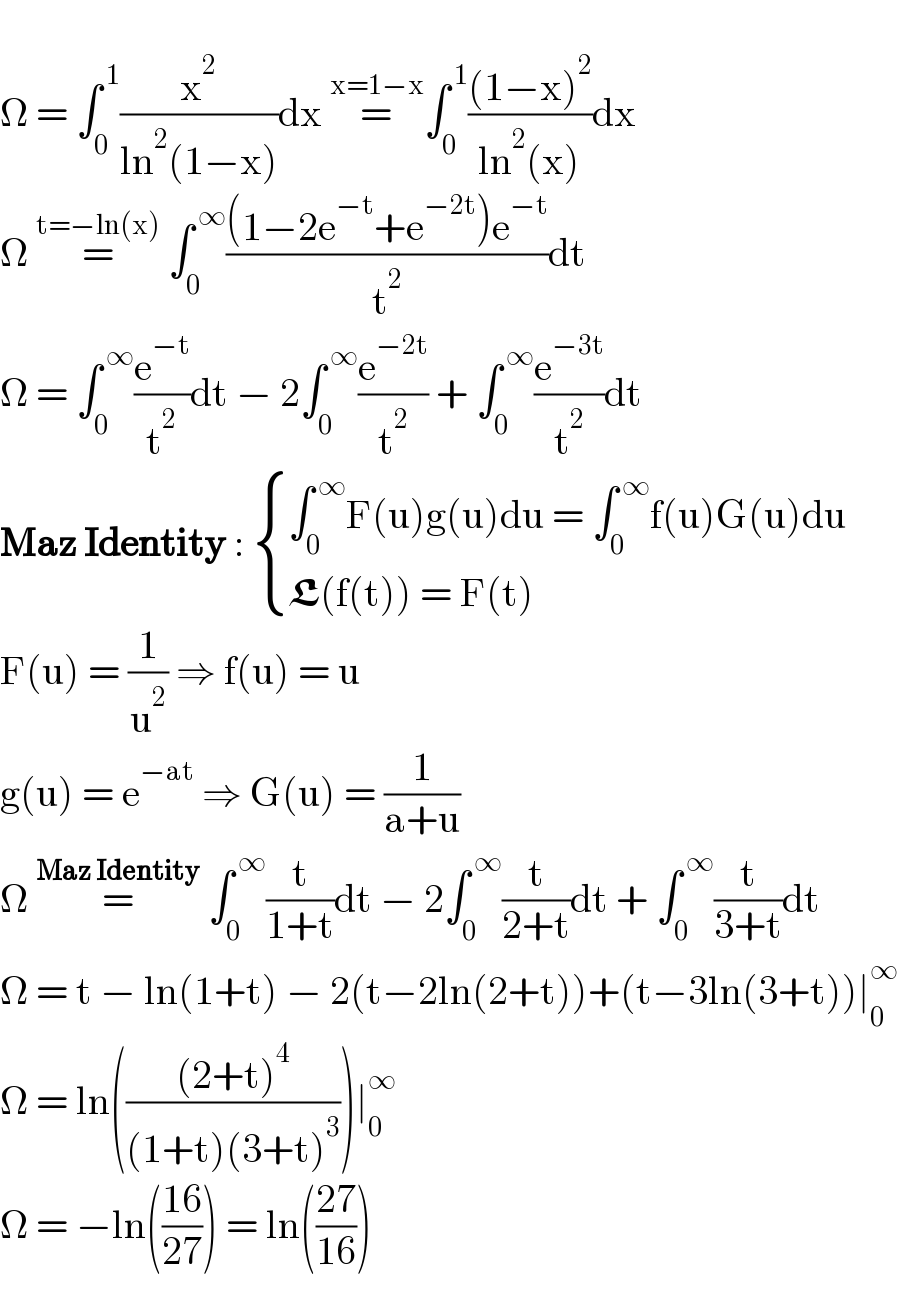
Ω = ∫_0 ^( 1) (x^2 /(ln^2 (1−x)))dx =^(x=1−x) ∫_0 ^( 1) (((1−x)^2 )/(ln^2 (x)))dx Ω =^(t=−ln(x)) ∫_0 ^( ∞) (((1−2e^(−t) +e^(−2t) )e^(−t) )/t^2 )dt Ω = ∫_0 ^( ∞) (e^(−t) /t^2 )dt − 2∫_0 ^( ∞) (e^(−2t) /t^2 ) + ∫_0 ^( ∞) (e^(−3t) /t^2 )dt Maz Identity : { ((∫_0 ^( ∞) F(u)g(u)du = ∫_0 ^( ∞) f(u)G(u)du)),((L(f(t)) = F(t))) :} F(u) = (1/u^2 ) ⇒ f(u) = u g(u) = e^(−at) ⇒ G(u) = (1/(a+u)) Ω =^(Maz Identity) ∫_0 ^( ∞) (t/(1+t))dt − 2∫_0 ^( ∞) (t/(2+t))dt + ∫_0 ^( ∞) (t/(3+t))dt Ω = t − ln(1+t) − 2(t−2ln(2+t))+(t−3ln(3+t))∣_0 ^∞ Ω = ln((((2+t)^4 )/((1+t)(3+t)^3 )))∣_0 ^∞ Ω = −ln(((16)/(27))) = ln(((27)/(16)))
$$ \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{1}−\mathrm{x}\right)}\mathrm{dx}\:\overset{\mathrm{x}=\mathrm{1}−\mathrm{x}} {=}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\left(\mathrm{1}−\mathrm{x}\right)^{\mathrm{2}} }{\mathrm{ln}^{\mathrm{2}} \left(\mathrm{x}\right)}\mathrm{dx} \\ $$$$\Omega\:\overset{\mathrm{t}=−\mathrm{ln}\left(\mathrm{x}\right)} {=}\:\int_{\mathrm{0}} ^{\:\infty} \frac{\left(\mathrm{1}−\mathrm{2e}^{−\mathrm{t}} +\mathrm{e}^{−\mathrm{2t}} \right)\mathrm{e}^{−\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{e}^{−\mathrm{t}} }{\mathrm{t}^{\mathrm{2}} }\mathrm{dt}\:−\:\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{e}^{−\mathrm{2t}} }{\mathrm{t}^{\mathrm{2}} }\:+\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{e}^{−\mathrm{3t}} }{\mathrm{t}^{\mathrm{2}} }\mathrm{dt} \\ $$$$\boldsymbol{\mathrm{Maz}}\:\boldsymbol{\mathrm{Identity}}\::\:\begin{cases}{\int_{\mathrm{0}} ^{\:\infty} \mathrm{F}\left(\mathrm{u}\right)\mathrm{g}\left(\mathrm{u}\right)\mathrm{du}\:=\:\int_{\mathrm{0}} ^{\:\infty} \mathrm{f}\left(\mathrm{u}\right)\mathrm{G}\left(\mathrm{u}\right)\mathrm{du}}\\{\boldsymbol{\mathfrak{L}}\left(\mathrm{f}\left(\mathrm{t}\right)\right)\:=\:\mathrm{F}\left(\mathrm{t}\right)}\end{cases} \\ $$$$\mathrm{F}\left(\mathrm{u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{u}^{\mathrm{2}} }\:\Rightarrow\:\mathrm{f}\left(\mathrm{u}\right)\:=\:\mathrm{u} \\ $$$$\mathrm{g}\left(\mathrm{u}\right)\:=\:\mathrm{e}^{−\mathrm{at}} \:\Rightarrow\:\mathrm{G}\left(\mathrm{u}\right)\:=\:\frac{\mathrm{1}}{\mathrm{a}+\mathrm{u}} \\ $$$$\Omega\:\overset{\boldsymbol{\mathrm{Maz}}\:\boldsymbol{\mathrm{Identity}}} {=}\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{t}}{\mathrm{1}+\mathrm{t}}\mathrm{dt}\:−\:\mathrm{2}\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{t}}{\mathrm{2}+\mathrm{t}}\mathrm{dt}\:+\:\int_{\mathrm{0}} ^{\:\infty} \frac{\mathrm{t}}{\mathrm{3}+\mathrm{t}}\mathrm{dt} \\ $$$$\Omega\:=\:\mathrm{t}\:−\:\mathrm{ln}\left(\mathrm{1}+\mathrm{t}\right)\:−\:\mathrm{2}\left(\mathrm{t}−\mathrm{2ln}\left(\mathrm{2}+\mathrm{t}\right)\right)+\left(\mathrm{t}−\mathrm{3ln}\left(\mathrm{3}+\mathrm{t}\right)\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$$\Omega\:=\:\mathrm{ln}\left(\frac{\left(\mathrm{2}+\mathrm{t}\right)^{\mathrm{4}} }{\left(\mathrm{1}+\mathrm{t}\right)\left(\mathrm{3}+\mathrm{t}\right)^{\mathrm{3}} }\right)\mid_{\mathrm{0}} ^{\infty} \\ $$$$\Omega\:=\:−\mathrm{ln}\left(\frac{\mathrm{16}}{\mathrm{27}}\right)\:=\:\mathrm{ln}\left(\frac{\mathrm{27}}{\mathrm{16}}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *