Question Number 79222 by mind is power last updated on 23/Jan/20
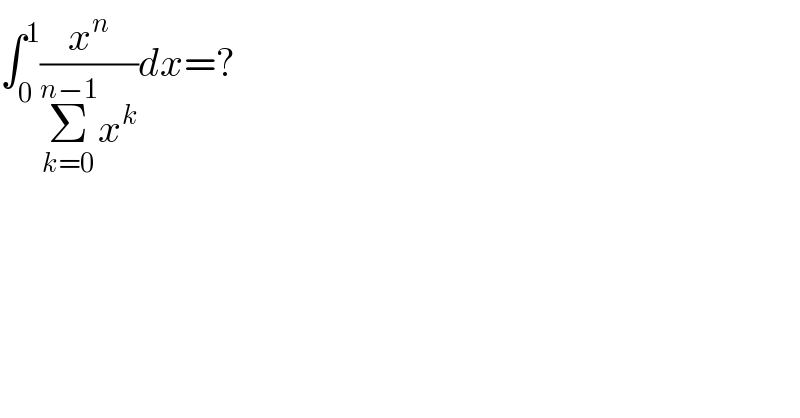
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{{n}} }{\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\sum}}{x}^{{k}} }{dx}=? \\ $$
Commented by mathmax by abdo last updated on 24/Jan/20
![at form of serie let A_n =∫_0 ^1 (x^n /(Σ_(k=0) ^(n−1) x^k ))dx ⇒ A_n =∫_0 ^1 (x^n /(x^(n−1) /(x−1)))dx =∫_0 ^1 ((x^n (x−1))/(x^n −1))dx =∫_0 ^1 ((x^(n+1) −x^n )/(x^n −1))dx =∫_0 ^1 (x^(n+1) −x^n )Σ_(k=0) ^∞ x^(kn) =Σ_(k=0) ^∞ ∫_0 ^1 (x^(n+1+kn) −x^(n+kn) )dx =Σ_(k=0) ^∞ ∫_0 ^1 (x^((k+1)n+1) −x^((k+1)n) )dx =Σ_(k=0) ^∞ [(1/((k+1)n+2))x^((k+1)n+2) −(1/((k+1)n +1))x^((k+1)n +1) ]_0 ^1 =Σ_(k=0) ^∞ {(1/((k+1)n+2)) −(1/((k+1)n +1))}=Σ_(k=1) ^∞ {(1/(kn+2))−(1/(kn +1))} =−Σ_(k=1) ^∞ (1/((kn +1)(kn +2))) be continued...(rest value of this serie!)](https://www.tinkutara.com/question/Q79267.png)
$${at}\:{form}\:{of}\:{serie}\:\:{let}\:{A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{n}} }{\sum_{{k}=\mathrm{0}} ^{{n}−\mathrm{1}} \:{x}^{{k}} }{dx}\:\Rightarrow \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{n}} }{\frac{{x}^{{n}−\mathrm{1}} }{{x}−\mathrm{1}}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{n}} \left({x}−\mathrm{1}\right)}{{x}^{{n}} −\mathrm{1}}{dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{{x}^{{n}+\mathrm{1}} −{x}^{{n}} }{{x}^{{n}} −\mathrm{1}}{dx} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \left({x}^{{n}+\mathrm{1}} −{x}^{{n}} \right)\sum_{{k}=\mathrm{0}} ^{\infty} \:{x}^{{kn}} \:=\sum_{{k}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({x}^{{n}+\mathrm{1}+{kn}} −{x}^{{n}+{kn}} \right){dx} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\left({x}^{\left({k}+\mathrm{1}\right){n}+\mathrm{1}} −{x}^{\left({k}+\mathrm{1}\right){n}} \right){dx} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\infty} \left[\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right){n}+\mathrm{2}}{x}^{\left({k}+\mathrm{1}\right){n}+\mathrm{2}} −\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right){n}\:+\mathrm{1}}{x}^{\left({k}+\mathrm{1}\right){n}\:+\mathrm{1}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\sum_{{k}=\mathrm{0}} ^{\infty} \left\{\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right){n}+\mathrm{2}}\:−\frac{\mathrm{1}}{\left({k}+\mathrm{1}\right){n}\:+\mathrm{1}}\right\}=\sum_{{k}=\mathrm{1}} ^{\infty} \left\{\frac{\mathrm{1}}{{kn}+\mathrm{2}}−\frac{\mathrm{1}}{{kn}\:+\mathrm{1}}\right\} \\ $$$$=−\sum_{{k}=\mathrm{1}} ^{\infty} \:\:\frac{\mathrm{1}}{\left({kn}\:+\mathrm{1}\right)\left({kn}\:+\mathrm{2}\right)}\:\:\:{be}\:{continued}…\left({rest}\:{value}\:{of}\:{this}\:{serie}!\right) \\ $$
Commented by mind is power last updated on 24/Jan/20
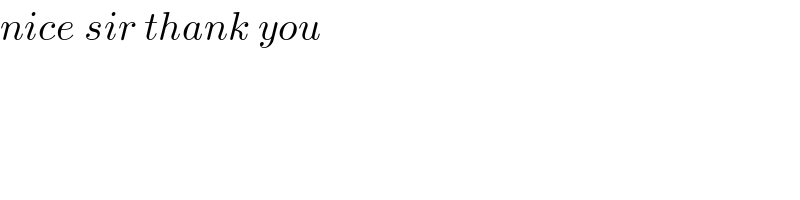
$${nice}\:{sir}\:{thank}\:{you} \\ $$
Commented by abdomathmax last updated on 24/Jan/20

$${you}\:{are}\:{welcome} \\ $$
