Question Number 154192 by mnjuly1970 last updated on 15/Sep/21
![Ω :=∫_0 ^( 1) (( x.sin(ln(x)))/(1−x))dx method 1 Ω= Im[∫_0 ^( 1) (( x^( i+1) )/(1−x)) dx=Φ] Φ = ∫_0 ^( 1) (( x^( i+1) +x^( i+2) )/(1−x^( 2) ))dx =^(x^( 2) =t) (1/2)∫_0 ^( 1) (( t^( (i/2)) −t^((i+1)/2) )/(1−t))dt = (1/2) { ψ (1 +((i+1)/2))−ψ (1+(i/2))} = (1/2) { (2/(1+i)) + ψ ( ((1+i)/2) )−(2/i)−ψ ((i/2))} = ((−i)/(−1+i)) + (1/2) {ψ (((1+i)/2))−ψ((i/2) )} = −(1/2) +(i/(2 )) +(1/2) {ψ(((1+i)/2))−ψ((i/2))} Ω = Im (Φ )= (1/2) +(1/2) Im(ψ((1/2) +(i/2)))−(1/2) Im((i/2)) = (1/(2 )) { 1 +(π/2) tanh((π/2)) −1−(π/2) coth((π/2))} =(π/4) {((−1)/(sinh((π/2)).cosh((π/2))))}=((−π)/(2 sinh (π ))) ✓](https://www.tinkutara.com/question/Q154192.png)
$$ \\ $$$$ \\ $$$$\:\:\:\:\:\:\:\Omega\::=\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{x}.{sin}\left({ln}\left({x}\right)\right)}{\mathrm{1}−{x}}{dx} \\ $$$$\:\:\:\:\:\:\:\:\:{method}\:\mathrm{1} \\ $$$$\:\:\:\:\:\Omega=\:\mathrm{I}{m}\left[\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:\:{x}^{\:{i}+\mathrm{1}} }{\mathrm{1}−{x}}\:{dx}=\Phi\right] \\ $$$$\:\:\:\:\:\:\:\:\:\Phi\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{x}^{\:{i}+\mathrm{1}} +{x}^{\:{i}+\mathrm{2}} }{\mathrm{1}−{x}^{\:\mathrm{2}} }{dx} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\overset{{x}^{\:\mathrm{2}} ={t}} {=}\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{t}^{\:\frac{{i}}{\mathrm{2}}} −{t}^{\frac{{i}+\mathrm{1}}{\mathrm{2}}} }{\mathrm{1}−{t}}{dt} \\ $$$$\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\:\psi\:\left(\mathrm{1}\:+\frac{{i}+\mathrm{1}}{\mathrm{2}}\right)−\psi\:\left(\mathrm{1}+\frac{{i}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\:\:\frac{\mathrm{2}}{\mathrm{1}+{i}}\:+\:\psi\:\left(\:\frac{\mathrm{1}+{i}}{\mathrm{2}}\:\right)−\frac{\mathrm{2}}{{i}}−\psi\:\left(\frac{{i}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:\:=\:\frac{−{i}}{−\mathrm{1}+{i}}\:\:+\:\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\psi\:\left(\frac{\mathrm{1}+{i}}{\mathrm{2}}\right)−\psi\left(\frac{{i}}{\mathrm{2}}\:\right)\right\} \\ $$$$\:\:\:=\:−\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{{i}}{\mathrm{2}\:}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\left\{\psi\left(\frac{\mathrm{1}+{i}}{\mathrm{2}}\right)−\psi\left(\frac{{i}}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:\Omega\:=\:\mathrm{I}{m}\:\left(\Phi\:\right)=\:\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{I}{m}\left(\psi\left(\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{{i}}{\mathrm{2}}\right)\right)−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{I}{m}\left(\frac{{i}}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\frac{\mathrm{1}}{\mathrm{2}\:}\:\left\{\:\mathrm{1}\:+\frac{\pi}{\mathrm{2}}\:{tanh}\left(\frac{\pi}{\mathrm{2}}\right)\:−\mathrm{1}−\frac{\pi}{\mathrm{2}}\:{coth}\left(\frac{\pi}{\mathrm{2}}\right)\right\} \\ $$$$\:\:\:\:\:\:=\frac{\pi}{\mathrm{4}}\:\:\left\{\frac{−\mathrm{1}}{{sinh}\left(\frac{\pi}{\mathrm{2}}\right).{cosh}\left(\frac{\pi}{\mathrm{2}}\right)}\right\}=\frac{−\pi}{\mathrm{2}\:{sinh}\:\left(\pi\:\right)}\:\checkmark \\ $$$$ \\ $$
Answered by qaz last updated on 15/Sep/21
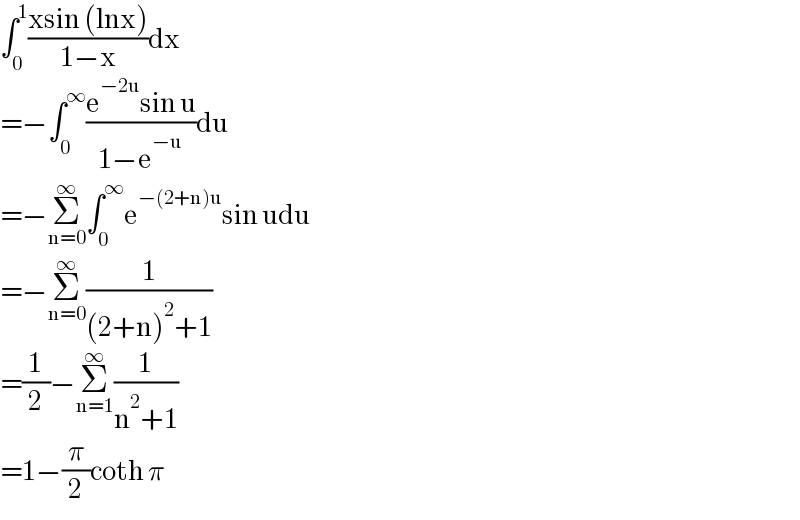
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{xsin}\:\left(\mathrm{lnx}\right)}{\mathrm{1}−\mathrm{x}}\mathrm{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{e}^{−\mathrm{2u}} \mathrm{sin}\:\mathrm{u}}{\mathrm{1}−\mathrm{e}^{−\mathrm{u}} }\mathrm{du} \\ $$$$=−\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\int_{\mathrm{0}} ^{\infty} \mathrm{e}^{−\left(\mathrm{2}+\mathrm{n}\right)\mathrm{u}} \mathrm{sin}\:\mathrm{udu} \\ $$$$=−\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{n}\right)^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{n}^{\mathrm{2}} +\mathrm{1}} \\ $$$$=\mathrm{1}−\frac{\pi}{\mathrm{2}}\mathrm{coth}\:\pi \\ $$
