Question Number 17010 by arnabpapu550@gmail.com last updated on 29/Jun/17
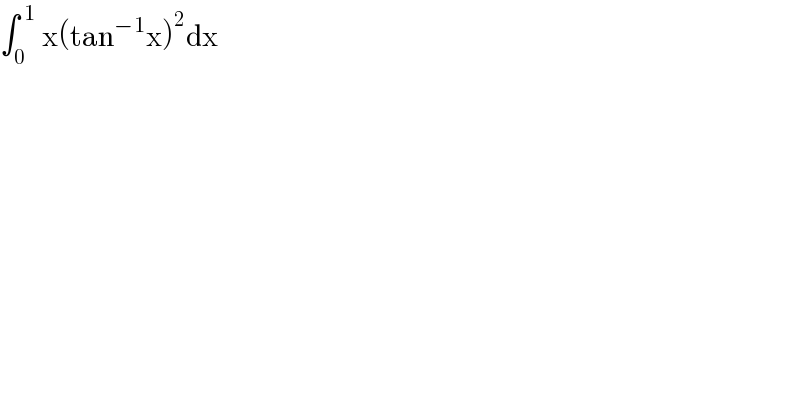
$$\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\mathrm{x}\left(\mathrm{tan}^{−\mathrm{1}} \mathrm{x}\right)^{\mathrm{2}} \mathrm{dx} \\ $$
Answered by sma3l2996 last updated on 29/Jun/17
![I=∫_0 ^1 x.(tan^(−1) (x))^2 dx u=(tan^(−1) (x))^2 ⇒u′=2((tan^(−1) x)/(x^2 +1)) v′=x⇒v=(x^2 /2) I=(1/2)[x^2 .(tan^(−1) x)^2 ]_0 ^1 −∫_0 ^1 (x^2 /(x^2 +1))tan^(−1) (x)dx =(π^2 /(32))−∫_0 ^1 (1−(1/(x^2 +1)))tan^(−1) (x)dx =(π^2 /(32))−∫_0 ^1 tan^(−1) (x)dx+∫_0 ^1 ((tan^(−1) x)/(x^2 +1))dx =(π^2 /(32))−[x.tan^(−1) x]_0 ^1 +∫_0 ^1 (x/(x^2 +1))dx+(1/2)[(tan^(−1) x)^2 ]_0 ^1 =(π^2 /(32))−(π/4)+(1/2)[ln(x^2 +1)]_0 ^1 +(π^2 /(32))−(π^2 /8) =((−π^2 )/(16))−(π/4)+(1/2)ln2 I=ln((√2))−(π^2 /(16))−(π/4)](https://www.tinkutara.com/question/Q17025.png)
$${I}=\int_{\mathrm{0}} ^{\mathrm{1}} {x}.\left({tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} {dx} \\ $$$${u}=\left({tan}^{−\mathrm{1}} \left({x}\right)\right)^{\mathrm{2}} \Rightarrow{u}'=\mathrm{2}\frac{{tan}^{−\mathrm{1}} {x}}{{x}^{\mathrm{2}} +\mathrm{1}} \\ $$$${v}'={x}\Rightarrow{v}=\frac{{x}^{\mathrm{2}} }{\mathrm{2}} \\ $$$${I}=\frac{\mathrm{1}}{\mathrm{2}}\left[{x}^{\mathrm{2}} .\left({tan}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} +\mathrm{1}}{tan}^{−\mathrm{1}} \left({x}\right){dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{32}}−\int_{\mathrm{0}} ^{\mathrm{1}} \left(\mathrm{1}−\frac{\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\right){tan}^{−\mathrm{1}} \left({x}\right){dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{32}}−\int_{\mathrm{0}} ^{\mathrm{1}} {tan}^{−\mathrm{1}} \left({x}\right){dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{tan}^{−\mathrm{1}} {x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{32}}−\left[{x}.{tan}^{−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} +\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{{x}^{\mathrm{2}} +\mathrm{1}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\left[\left({tan}^{−\mathrm{1}} {x}\right)^{\mathrm{2}} \right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{32}}−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}\left({x}^{\mathrm{2}} +\mathrm{1}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\frac{\pi^{\mathrm{2}} }{\mathrm{32}}−\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$$=\frac{−\pi^{\mathrm{2}} }{\mathrm{16}}−\frac{\pi}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{2}}{ln}\mathrm{2} \\ $$$${I}={ln}\left(\sqrt{\mathrm{2}}\right)−\frac{\pi^{\mathrm{2}} }{\mathrm{16}}−\frac{\pi}{\mathrm{4}} \\ $$
