Question Number 176542 by mnjuly1970 last updated on 20/Sep/22
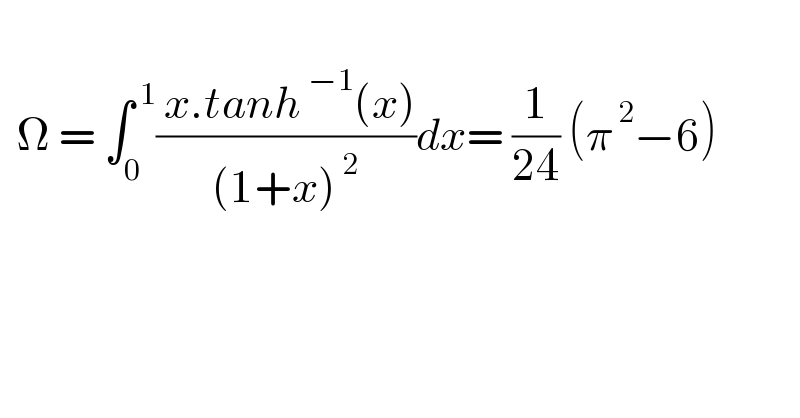
$$ \\ $$$$\:\:\Omega\:=\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\:{x}.{tanh}^{\:−\mathrm{1}} \left({x}\right)}{\left(\mathrm{1}+{x}\right)^{\:\mathrm{2}} }{dx}=\:\frac{\mathrm{1}}{\mathrm{24}}\:\left(\pi^{\:\mathrm{2}} −\mathrm{6}\right) \\ $$
Answered by Peace last updated on 20/Sep/22
![∫_0 ^1 (x/((1+x)^2 ))tg^− (x)dx tanh^− (x)=(1/2)(ln(1+x)−ln(1−x)) (x/((1+x)^2 ))=(1/(1+x))−(1/((1+x)^2 )) 2Ω=∫_0 ^1 ((ln(1+x))/(1+x))−((ln(1+x))/((1+x)^2 ))dx+∫_0 ^1 ((ln(1−x))/((1+x)^2 ))dx−∫_0 ^1 ((ln(1−x))/(1+x))dx =(1/2)[ln^2 (1+x)]_0 ^1 +[((ln(1+x))/(1+x))]_0 ^1 −∫_0 ^1 (1/((1+x)^2 ))+A+B =((ln^2 (2))/2)+((ln(2))/2)+(1/2)+A+B A=lim_(x→1) ∫_0 ^x ((ln(1−t))/((1+t)^2 ))dt=lim_(x→1) {−((ln(1−x))/(1+x))−∫_0 ^x (1/(1−t^2 )).dt} =lim_(x→1) −((ln(1−x))/(1+x))−(1/2)∫_0 ^x (1/(1−t))+(1/(1+t))dt =lim_(x→1) −((ln(1−x))/(1+x))+((ln(1−x))/2)−((ln(1+x))/2) =−((ln(2))/2) −B=∫_0 ^1 ((ln(1−x))/(1+x))dx x=((1−t)/(1+t)),=−1+(2/(1+t))⇒dt=−((2dt)/((1+t)^2 )) 2∫_0 ^1 ((ln(((2t)/(1+t))))/(2/((1+t)))).(1/((1+t)^2 ))dt=∫_0 ^1 ((ln(2t)−ln(1+t))/(1+t))dt =∫_0 ^1 ((ln(2))/(1+t))+((ln(t))/(1+t))−((ln(1+t))/(1+t))dt =ln^2 (2)−((ln^2 (2))/2)+∫_0 ^1 ((ln(t))/(1+t))dt=((ln^2 (2))/2)+∫_0 ^1 ((ln(1−(−t))/(−t))d(−t) =((ln^2 (2))/2)−Li_2 (−1) B=−((ln^2 (2))/2)+Li_2 (−1) 2Ω=((ln^2 (2))/2)+((ln(2))/2)+(1/2)+A+B =((ln^2 (2))/2)+((ln(2))/2)+(1/2)−((ln(2))/2)−((ln^2 (2))/2)+Li_2 (−1) =(1/2)+Li_2 (−1)=(1/2)+(π^2 /(12))=(1/(12))(π^2 −6) Ω=(1/(24))(π^2 −6)](https://www.tinkutara.com/question/Q176545.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{tg}^{−} \left({x}\right){dx} \\ $$$${tanh}^{−} \left({x}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\mathrm{1}+{x}\right)−{ln}\left(\mathrm{1}−{x}\right)\right) \\ $$$$\frac{{x}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}\Omega=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}−\frac{{ln}\left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }{dx}−\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[{ln}^{\mathrm{2}} \left(\mathrm{1}+{x}\right)\right]_{\mathrm{0}} ^{\mathrm{1}} +\left[\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{1}+{x}}\right]_{\mathrm{0}} ^{\mathrm{1}} −\int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\left(\mathrm{1}+{x}\right)^{\mathrm{2}} }+{A}+{B} \\ $$$$=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+{A}+{B} \\ $$$${A}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\int_{\mathrm{0}} ^{{x}} \frac{{ln}\left(\mathrm{1}−{t}\right)}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}\left\{−\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}−\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }.{dt}\right\} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}−\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}−\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{0}} ^{{x}} \frac{\mathrm{1}}{\mathrm{1}−{t}}+\frac{\mathrm{1}}{\mathrm{1}+{t}}{dt} \\ $$$$=\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}−\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}+\frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{2}}−\frac{{ln}\left(\mathrm{1}+{x}\right)}{\mathrm{2}} \\ $$$$=−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}} \\ $$$$−{B}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−{x}\right)}{\mathrm{1}+{x}}{dx} \\ $$$${x}=\frac{\mathrm{1}−{t}}{\mathrm{1}+{t}},=−\mathrm{1}+\frac{\mathrm{2}}{\mathrm{1}+{t}}\Rightarrow{dt}=−\frac{\mathrm{2}{dt}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} } \\ $$$$\mathrm{2}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\frac{\mathrm{2}{t}}{\mathrm{1}+{t}}\right)}{\frac{\mathrm{2}}{\left(\mathrm{1}+{t}\right)}}.\frac{\mathrm{1}}{\left(\mathrm{1}+{t}\right)^{\mathrm{2}} }{dt}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{2}{t}\right)−{ln}\left(\mathrm{1}+{t}\right)}{\mathrm{1}+{t}}{dt} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{2}\right)}{\mathrm{1}+{t}}+\frac{{ln}\left({t}\right)}{\mathrm{1}+{t}}−\frac{{ln}\left(\mathrm{1}+{t}\right)}{\mathrm{1}+{t}}{dt} \\ $$$$={ln}^{\mathrm{2}} \left(\mathrm{2}\right)−\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\boldsymbol{{t}}\right)}{\mathrm{1}+{t}}{dt}=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{ln}\left(\mathrm{1}−\left(−{t}\right)\right.}{−{t}}{d}\left(−{t}\right) \\ $$$$=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}−{Li}_{\mathrm{2}} \left(−\mathrm{1}\right) \\ $$$${B}=−\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+{Li}_{\mathrm{2}} \left(−\mathrm{1}\right) \\ $$$$\mathrm{2}\Omega=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}+{A}+{B} \\ $$$$=\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\frac{{ln}\left(\mathrm{2}\right)}{\mathrm{2}}−\frac{{ln}^{\mathrm{2}} \left(\mathrm{2}\right)}{\mathrm{2}}+{Li}_{\mathrm{2}} \left(−\mathrm{1}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+{Li}_{\mathrm{2}} \left(−\mathrm{1}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\pi^{\mathrm{2}} }{\mathrm{12}}=\frac{\mathrm{1}}{\mathrm{12}}\left(\pi^{\mathrm{2}} −\mathrm{6}\right) \\ $$$$\Omega=\frac{\mathrm{1}}{\mathrm{24}}\left(\pi^{\mathrm{2}} −\mathrm{6}\right) \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by Tawa11 last updated on 22/Sep/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
Commented by Peace last updated on 23/Sep/22
$${thank}\:{You}\:{nice}\:{Day} \\ $$
