Question Number 156194 by talminator2856791 last updated on 09/Oct/21
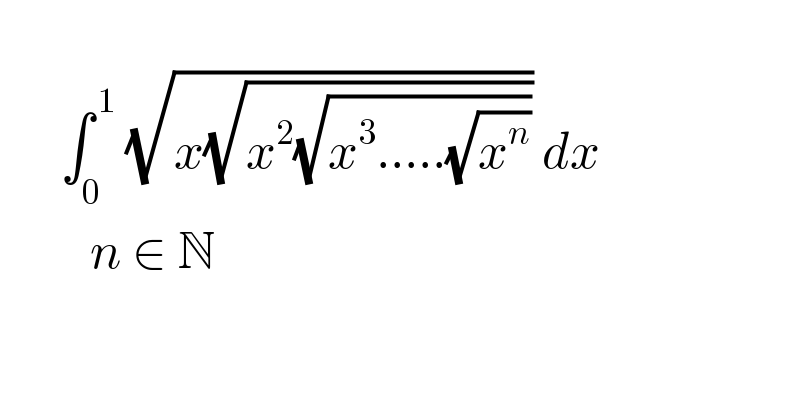
$$\: \\ $$$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{1}} \:\sqrt{{x}\sqrt{{x}^{\mathrm{2}} \sqrt{{x}^{\mathrm{3}} …..\sqrt{{x}^{{n}} }}}}\:{dx} \\ $$$$\:\:\:\:\:\:\:\:\:{n}\:\in\:\mathbb{N} \\ $$$$\: \\ $$
Commented by MJS_new last updated on 10/Oct/21
![=∫_0 ^1 x^(2−((n+2)/2^n )) dx=[(x^(3−((n+2)/2^n )) /(3−((n+2)/2^n )))]_0 ^1 =(2^n /(3×2^n −n−2))](https://www.tinkutara.com/question/Q156294.png)
$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}{x}^{\mathrm{2}−\frac{{n}+\mathrm{2}}{\mathrm{2}^{{n}} }} {dx}=\left[\frac{{x}^{\mathrm{3}−\frac{{n}+\mathrm{2}}{\mathrm{2}^{{n}} }} }{\mathrm{3}−\frac{{n}+\mathrm{2}}{\mathrm{2}^{{n}} }}\right]_{\mathrm{0}} ^{\mathrm{1}} =\frac{\mathrm{2}^{{n}} }{\mathrm{3}×\mathrm{2}^{{n}} −{n}−\mathrm{2}} \\ $$
