Question Number 58222 by salahahmed last updated on 20/Apr/19

$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{x}} {dx} \\ $$
Commented by maxmathsup by imad last updated on 21/Apr/19
![we have x^x =e^(xln(x)) ⇒∫_0 ^1 x^x dx =∫_0 ^1 (Σ_(n=0) ^∞ ((x^n (ln(x))^n )/(n!)))dx =Σ_(n=0) ^∞ (1/(n!)) ∫_0 ^1 x^n (ln(x))^n dx let A_(n,p) =∫_0 ^1 x^n (ln(x))^p dx by parts u^′ =x^n and v =(ln(x))^p ⇒u =(1/(n+1))x^(n+1) and v^′ =(p/x)(ln(x))^(p−1) ⇒ A_(n,p) =[(1/(n+1))x^(n+1) (ln(x))^p ]_0 ^1 −∫_0 ^1 (1/(n+1))x^(n+1) (p/x) (ln(x))^(p−1) dx =−(p/(n+1)) ∫_0 ^1 x^n (ln(x))^(p−1) =−(p/(n+1)) A_(n,p−1) =(((−1)^2 p(p−1))/((n+1)^2 )) A_(n,p−2) =(((−1)^p p!)/((n+1)^p )) A_(n,0) but A_(n,o) = ∫_0 ^1 x^n =(1/(n+1)) ⇒ A_(n,p) =(((−1)^p p!)/((n+1)^(p+1) )) ⇒A_(n,n) = (((−1)^n n!)/((n+1)^(n+1) )) ⇒ ∫_0 ^1 x^x dx =Σ_(n=0) ^∞ (((−1)^n )/((n+1)^(n+1) )) =1−(1/2^2 ) +(1/3^3 ) −(1/4^4 ) +....](https://www.tinkutara.com/question/Q58315.png)
$${we}\:{have}\:{x}^{{x}} \:={e}^{{xln}\left({x}\right)} \:\Rightarrow\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{x}} {dx}\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\left(\sum_{{n}=\mathrm{0}} ^{\infty} \:\frac{{x}^{{n}} \left({ln}\left({x}\right)\right)^{{n}} }{{n}!}\right){dx} \\ $$$$=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\frac{\mathrm{1}}{{n}!}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \left({ln}\left({x}\right)\right)^{{n}} \:{dx}\:\:{let}\:{A}_{{n},{p}} =\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \left({ln}\left({x}\right)\right)^{{p}} {dx}\:\:\:{by}\:{parts}\: \\ $$$${u}^{'} \:={x}^{{n}} \:{and}\:{v}\:=\left({ln}\left({x}\right)\right)^{{p}} \:\Rightarrow{u}\:=\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:{and}\:{v}^{'} \:=\frac{{p}}{{x}}\left({ln}\left({x}\right)\right)^{{p}−\mathrm{1}} \:\Rightarrow \\ $$$${A}_{{n},{p}} \:=\left[\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:\left({ln}\left({x}\right)\right)^{{p}} \right]_{\mathrm{0}} ^{\mathrm{1}} \:−\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{1}}{{n}+\mathrm{1}}{x}^{{n}+\mathrm{1}} \:\frac{{p}}{{x}}\:\left({ln}\left({x}\right)\right)^{{p}−\mathrm{1}} \:{dx} \\ $$$$=−\frac{{p}}{{n}+\mathrm{1}}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:\:\left({ln}\left({x}\right)\right)^{{p}−\mathrm{1}} \:=−\frac{{p}}{{n}+\mathrm{1}}\:{A}_{{n},{p}−\mathrm{1}} \:=\frac{\left(−\mathrm{1}\right)^{\mathrm{2}} {p}\left({p}−\mathrm{1}\right)}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\:{A}_{{n},{p}−\mathrm{2}} \\ $$$$=\frac{\left(−\mathrm{1}\right)^{{p}} \:{p}!}{\left({n}+\mathrm{1}\right)^{{p}} }\:{A}_{{n},\mathrm{0}} \:\:\:\:\:{but}\:\:{A}_{{n},{o}} =\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{n}} \:=\frac{\mathrm{1}}{{n}+\mathrm{1}}\:\Rightarrow \\ $$$${A}_{{n},{p}} =\frac{\left(−\mathrm{1}\right)^{{p}} {p}!}{\left({n}+\mathrm{1}\right)^{{p}+\mathrm{1}} }\:\Rightarrow{A}_{{n},{n}} =\:\frac{\left(−\mathrm{1}\right)^{{n}} {n}!}{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{x}} \:{dx}\:=\sum_{{n}=\mathrm{0}} ^{\infty} \:\:\:\frac{\left(−\mathrm{1}\right)^{{n}} }{\left({n}+\mathrm{1}\right)^{{n}+\mathrm{1}} }\:=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\:+\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\:−\frac{\mathrm{1}}{\mathrm{4}^{\mathrm{4}} }\:+…. \\ $$
Commented by maxmathsup by imad last updated on 21/Apr/19
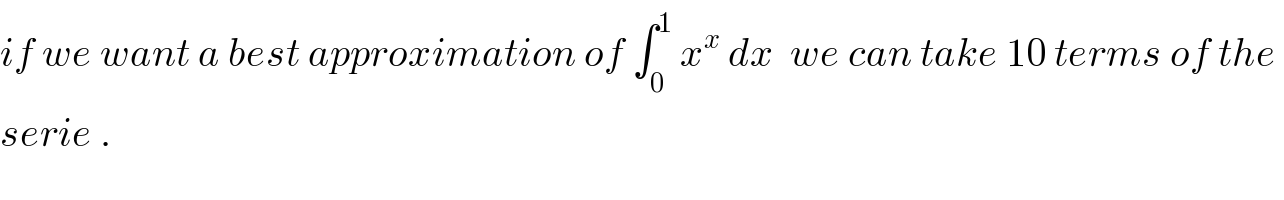
$${if}\:{we}\:{want}\:{a}\:{best}\:{approximation}\:{of}\:\int_{\mathrm{0}} ^{\mathrm{1}} \:{x}^{{x}} \:{dx}\:\:{we}\:{can}\:{take}\:\mathrm{10}\:{terms}\:{of}\:{the}\: \\ $$$${serie}\:. \\ $$
Commented by salahahmed last updated on 21/Apr/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by maxmathsup by imad last updated on 21/Apr/19
$${you}\:{are}\:{welcome}\:. \\ $$
Answered by Kunal12588 last updated on 20/Apr/19
![∫_0 ^1 x^x dx=[(x^(x+1) /(x+1))]_0 ^1 =(1^(1+1) /(1+1))−(0^(0+1) /(0+1)) =(1/2)−0=(1/2) is this correct?](https://www.tinkutara.com/question/Q58224.png)
$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{x}} \:{dx}=\left[\frac{{x}^{{x}+\mathrm{1}} }{{x}+\mathrm{1}}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}^{\mathrm{1}+\mathrm{1}} }{\mathrm{1}+\mathrm{1}}−\frac{\mathrm{0}^{\mathrm{0}+\mathrm{1}} }{\mathrm{0}+\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{0}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${is}\:{this}\:{correct}? \\ $$
Commented by mr W last updated on 20/Apr/19
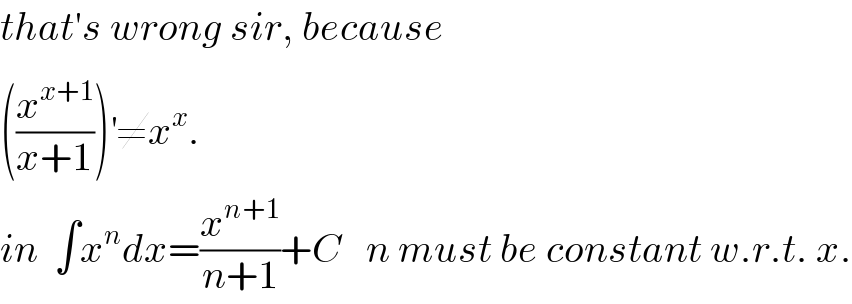
$${that}'{s}\:{wrong}\:{sir},\:{because} \\ $$$$\left(\frac{{x}^{{x}+\mathrm{1}} }{{x}+\mathrm{1}}\right)^{'} \neq{x}^{{x}} . \\ $$$${in}\:\:\int{x}^{{n}} {dx}=\frac{{x}^{{n}+\mathrm{1}} }{{n}+\mathrm{1}}+{C}\:\:\:{n}\:{must}\:{be}\:{constant}\:{w}.{r}.{t}.\:{x}. \\ $$
Commented by Kunal12588 last updated on 20/Apr/19
Ohh.. Thanks sir. So how can we solve that.
Answered by MJS last updated on 20/Apr/19

$$\approx.\mathrm{7834305109} \\ $$
Commented by salahahmed last updated on 20/Apr/19
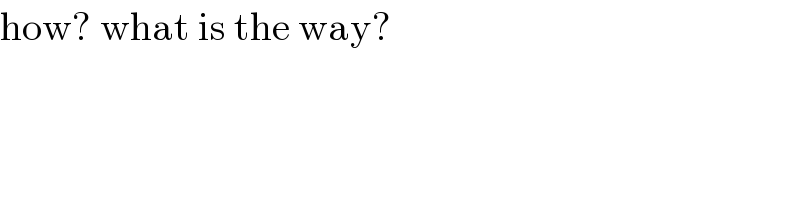
$$\mathrm{how}?\:\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{way}? \\ $$
Commented by MJS last updated on 20/Apr/19

$$\mathrm{you}\:\mathrm{can}\:\mathrm{only}\:\mathrm{approximate}\:\mathrm{by}\:\mathrm{lower}\:\mathrm{sums} \\ $$$$\mathrm{and}\:\mathrm{upper}\:\mathrm{sums} \\ $$
