Question Number 170549 by mathlove last updated on 26/May/22
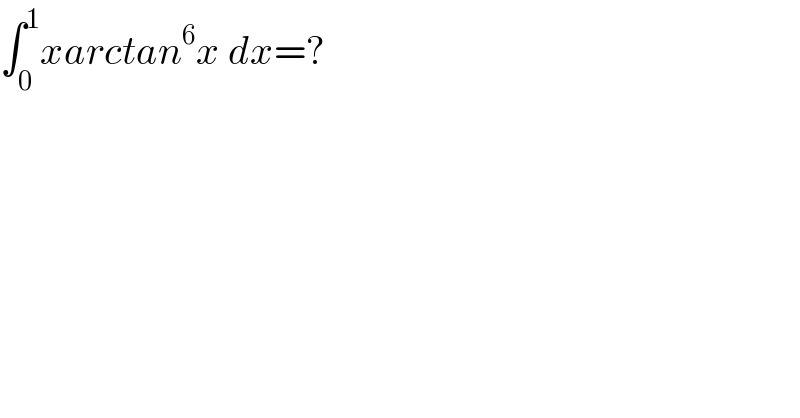
$$\int_{\mathrm{0}} ^{\mathrm{1}} {xarctan}^{\mathrm{6}} {x}\:{dx}=? \\ $$
Answered by Mathspace last updated on 26/May/22
![by ρarts I=[(x^2 /2)arctan^6 x]_0 ^1 − ∫_0 ^1 (x^2 /2) ((6arctanx^5 )/(1+x^2 ))dx =(1/2)((π^4 /6))−3∫_0 ^1 ((x^2 (arctanx)^5 )/(1+x^2 ))dx changement arctanx=θ give ∫_0 ^1 x^2 (((arctanx)^5 )/(1+x^2 ))dx =∫_0 ^(π/4) tan^2 θ×(θ^5 /(1+tan^2 θ))(1+tan^2 θ)dθ =∫_0 ^(π/4) x^5 tan^2 x dx =∫_0 ^(π/4) (1+tan^2 x−1)x^5 dx =∫_0 ^(π/4) x^5 (1+tan^2 x)−∫_0 ^(π/4) x^5 dx =−(1/6)((π/4))^6 +∫_0 ^(π/4) x^5 (1+tan^2 x)dx and ∫_0 ^(π/4) x^5 (1+tan^2 x)dx =[x^5 tanx]_0 ^(π/4) −∫_0 ^(π/4) 5x^4 tanx dx =((π/4))^5 −5∫_0 ^(π/4) x^4 tanx dx tanx=Σ a_(2n+1) x^(2n+1) =a_1 x +a_3 x^3 +... f(x)=tanx =Σ_i ((f^((i)) (0))/(i!))x^i f(o)=0 f^′ (x)=1+tan^2 x ⇒ f^′ (o)=1 f^((2)) (x)=2tanx(1+tan^2 x) ⇒ f^((2)) (0)=0 f^((3)) (0)=2(1+tan^2 x)(1+tan^2 x)+ 2tanx(....) ⇒f^((3)) (0)=2 ⇒ tanx=x +(2/(3!))x^3 +... =x+(x^3 /3)+... ⇒ ∫_0 ^(π/4) x^4 tanx dx=∫_0 ^(π/4) (x^5 +(x^4 /3)+...)dx =[(x^6 /6)+(x^5 /(15))+....]_0 ^(π/4) =(1/6)((π/4))^6 +(1/(15))((π/4))^5 +....](https://www.tinkutara.com/question/Q170559.png)
$${by}\:\rho{arts}\:\:{I}=\left[\frac{{x}^{\mathrm{2}} }{\mathrm{2}}{arctan}^{\mathrm{6}} {x}\right]_{\mathrm{0}} ^{\mathrm{1}} − \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} }{\mathrm{2}}\:\frac{\mathrm{6}{arctanx}^{\mathrm{5}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi^{\mathrm{4}} }{\mathrm{6}}\right)−\mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}^{\mathrm{2}} \left({arctanx}\right)^{\mathrm{5}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$${changement}\:{arctanx}=\theta\:{give} \\ $$$$\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} \frac{\left({arctanx}\right)^{\mathrm{5}} }{\mathrm{1}+{x}^{\mathrm{2}} }{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {tan}^{\mathrm{2}} \theta×\frac{\theta^{\mathrm{5}} }{\mathrm{1}+{tan}^{\mathrm{2}} \theta}\left(\mathrm{1}+{tan}^{\mathrm{2}} \theta\right){d}\theta \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}^{\mathrm{5}} {tan}^{\mathrm{2}} {x}\:{dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left(\mathrm{1}+{tan}^{\mathrm{2}} {x}−\mathrm{1}\right){x}^{\mathrm{5}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}^{\mathrm{5}} \left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)−\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}^{\mathrm{5}} {dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\pi}{\mathrm{4}}\right)^{\mathrm{6}} +\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}^{\mathrm{5}} \left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){dx} \\ $$$${and}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}^{\mathrm{5}} \left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right){dx} \\ $$$$=\left[{x}^{\mathrm{5}} {tanx}\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} −\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \mathrm{5}{x}^{\mathrm{4}} {tanx}\:{dx} \\ $$$$=\left(\frac{\pi}{\mathrm{4}}\right)^{\mathrm{5}} −\mathrm{5}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}^{\mathrm{4}} {tanx}\:{dx} \\ $$$${tanx}=\Sigma\:{a}_{\mathrm{2}{n}+\mathrm{1}} {x}^{\mathrm{2}{n}+\mathrm{1}} \\ $$$$={a}_{\mathrm{1}} {x}\:+{a}_{\mathrm{3}} {x}^{\mathrm{3}} +… \\ $$$${f}\left({x}\right)={tanx}\:=\sum_{{i}} \:\frac{{f}^{\left({i}\right)} \left(\mathrm{0}\right)}{{i}!}{x}^{{i}} \\ $$$${f}\left({o}\right)=\mathrm{0}\:\:{f}^{'} \left({x}\right)=\mathrm{1}+{tan}^{\mathrm{2}} {x}\:\Rightarrow \\ $$$${f}^{'} \left({o}\right)=\mathrm{1} \\ $$$${f}^{\left(\mathrm{2}\right)} \left({x}\right)=\mathrm{2}{tanx}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\:\Rightarrow \\ $$$${f}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\mathrm{0} \\ $$$${f}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=\mathrm{2}\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)\left(\mathrm{1}+{tan}^{\mathrm{2}} {x}\right)+ \\ $$$$\mathrm{2}{tanx}\left(….\right)\:\Rightarrow{f}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=\mathrm{2}\:\Rightarrow \\ $$$${tanx}={x}\:+\frac{\mathrm{2}}{\mathrm{3}!}{x}^{\mathrm{3}} +… \\ $$$$={x}+\frac{{x}^{\mathrm{3}} }{\mathrm{3}}+…\:\Rightarrow \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {x}^{\mathrm{4}} {tanx}\:{dx}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \left({x}^{\mathrm{5}} +\frac{{x}^{\mathrm{4}} }{\mathrm{3}}+…\right){dx} \\ $$$$=\left[\frac{{x}^{\mathrm{6}} }{\mathrm{6}}+\frac{{x}^{\mathrm{5}} }{\mathrm{15}}+….\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{6}}\left(\frac{\pi}{\mathrm{4}}\right)^{\mathrm{6}} +\frac{\mathrm{1}}{\mathrm{15}}\left(\frac{\pi}{\mathrm{4}}\right)^{\mathrm{5}} +…. \\ $$
Commented by Tawa11 last updated on 08/Oct/22

$$\mathrm{Great}\:\mathrm{sir} \\ $$
