Question Number 87711 by M±th+et£s last updated on 05/Apr/20
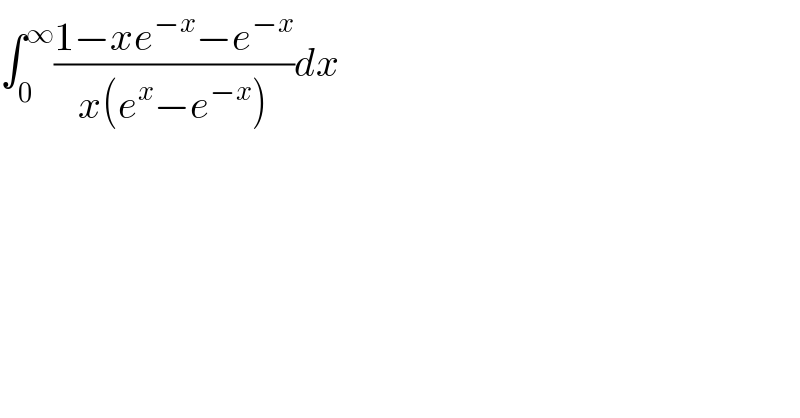
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{xe}^{−{x}} −{e}^{−{x}} }{{x}\left({e}^{{x}} −{e}^{−{x}} \right)}{dx} \\ $$
Commented by mind is power last updated on 05/Apr/20
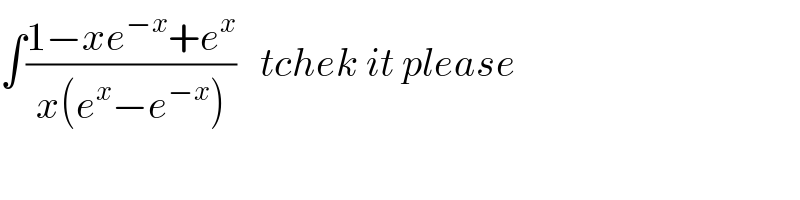
$$\int\frac{\mathrm{1}−{xe}^{−{x}} +{e}^{{x}} }{{x}\left({e}^{{x}} −{e}^{−{x}} \right)}\:\:\:{tchek}\:{it}\:{please} \\ $$
Commented by M±th+et£s last updated on 05/Apr/20
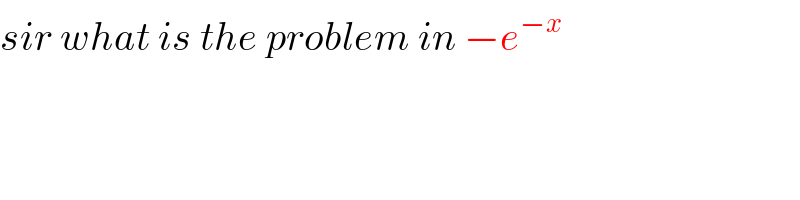
$${sir}\:{what}\:{is}\:{the}\:{problem}\:{in}\:−{e}^{−{x}} \\ $$
Answered by M±th+et£s last updated on 06/Apr/20
![∫_0 ^∞ ((1−xe^(−x) −e^(−x) )/(x(e^x −e^(−x) )))×((e^x /e^x ))dx =∫_(0 ) ^∞ ((e^x −x−1)/(x(e^(2x) −1)))dx=∫((Σ_(n=2) ^∞ (x^n /(n!)))/(x(e^(2x) −1)))dx =Σ_(n=2) ^∞ (1/(n!))∫_0 ^∞ (x^(n−1) /(x(e^(2x) −1)))dx=Σ_(n=2) ^∞ (1/(n!))(ζ(n)Γ(n)) =Σ_(n=2) ^∞ ((ζ(n))/(n2^n ))=Σ_(n=2) ^∞ (1/(n2^n ))Σ_(k=1) ^∞ (1/k^n ) Σ_(k=1) ^∞ Σ_(k=2) ^∞ (1/(n(2k)^2 ))=Σ_(k=1) ^∞ (ln(((2k)/(2k−1)))−(1/(2k))) lim_(n→∞) [ln((((2n)!!)/((2n−1)!)))−(H_n /2)] (1/2)lim_(n→∞) [ln(π)+ln(2)−H_n ]=(1/2)(ln(π)−γ)](https://www.tinkutara.com/question/Q87883.png)
$$\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{xe}^{−{x}} −{e}^{−{x}} }{{x}\left({e}^{{x}} −{e}^{−{x}} \right)}×\left(\frac{{e}^{{x}} }{{e}^{{x}} }\right){dx} \\ $$$$=\int_{\mathrm{0}\:} ^{\infty} \frac{{e}^{{x}} −{x}−\mathrm{1}}{{x}\left({e}^{\mathrm{2}{x}} −\mathrm{1}\right)}{dx}=\int\frac{\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{{x}^{{n}} }{{n}!}}{{x}\left({e}^{\mathrm{2}{x}} −\mathrm{1}\right)}{dx} \\ $$$$=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\int_{\mathrm{0}} ^{\infty} \frac{{x}^{{n}−\mathrm{1}} }{{x}\left({e}^{\mathrm{2}{x}} −\mathrm{1}\right)}{dx}=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}!}\left(\zeta\left({n}\right)\Gamma\left({n}\right)\right) \\ $$$$=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\zeta\left({n}\right)}{{n}\mathrm{2}^{{n}} }=\underset{{n}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{n}\mathrm{2}^{{n}} }\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{{k}^{{n}} } \\ $$$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{n}\left(\mathrm{2}{k}\right)^{\mathrm{2}} }=\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left({ln}\left(\frac{\mathrm{2}{k}}{\mathrm{2}{k}−\mathrm{1}}\right)−\frac{\mathrm{1}}{\mathrm{2}{k}}\right) \\ $$$$\underset{{n}\rightarrow\infty} {{lim}}\left[{ln}\left(\frac{\left(\mathrm{2}{n}\right)!!}{\left(\mathrm{2}{n}−\mathrm{1}\right)!}\right)−\frac{{H}_{{n}} }{\mathrm{2}}\right] \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\underset{{n}\rightarrow\infty} {{lim}}\left[{ln}\left(\pi\right)+{ln}\left(\mathrm{2}\right)−{H}_{{n}} \right]=\frac{\mathrm{1}}{\mathrm{2}}\left({ln}\left(\pi\right)−\gamma\right) \\ $$
