Question Number 125421 by bemath last updated on 11/Dec/20
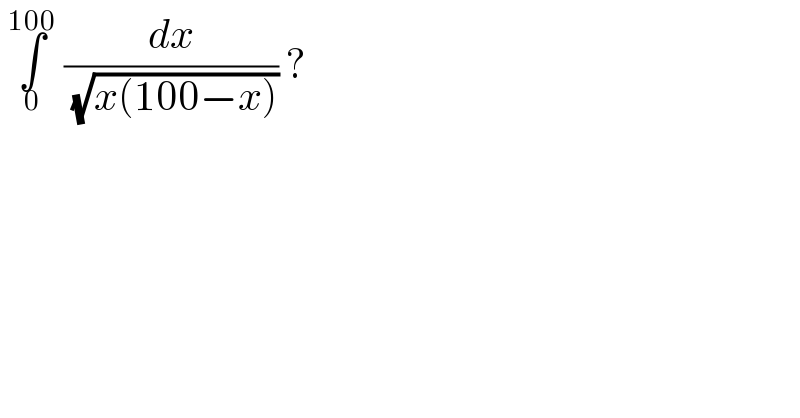
$$\:\underset{\mathrm{0}} {\overset{\mathrm{100}} {\int}}\:\frac{{dx}}{\:\sqrt{{x}\left(\mathrm{100}−{x}\right)}}\:?\: \\ $$
Answered by liberty last updated on 11/Dec/20
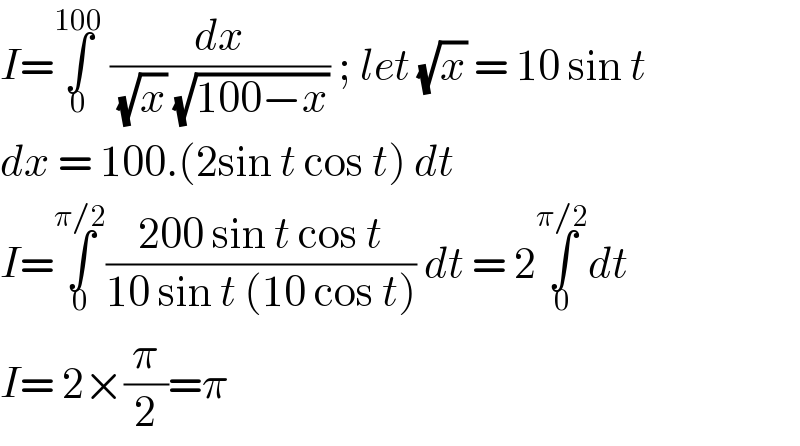
$${I}=\underset{\mathrm{0}} {\overset{\mathrm{100}} {\int}}\:\frac{{dx}}{\:\sqrt{{x}}\:\sqrt{\mathrm{100}−{x}}}\:;\:{let}\:\sqrt{{x}}\:=\:\mathrm{10}\:\mathrm{sin}\:{t}\: \\ $$$${dx}\:=\:\mathrm{100}.\left(\mathrm{2sin}\:{t}\:\mathrm{cos}\:{t}\right)\:{dt}\: \\ $$$${I}=\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}\frac{\mathrm{200}\:\mathrm{sin}\:{t}\:\mathrm{cos}\:{t}}{\mathrm{10}\:\mathrm{sin}\:{t}\:\left(\mathrm{10}\:\mathrm{cos}\:{t}\right)}\:{dt}\:=\:\mathrm{2}\underset{\mathrm{0}} {\overset{\pi/\mathrm{2}} {\int}}{dt}\: \\ $$$${I}=\:\mathrm{2}×\frac{\pi}{\mathrm{2}}=\pi \\ $$
Answered by Dwaipayan Shikari last updated on 11/Dec/20
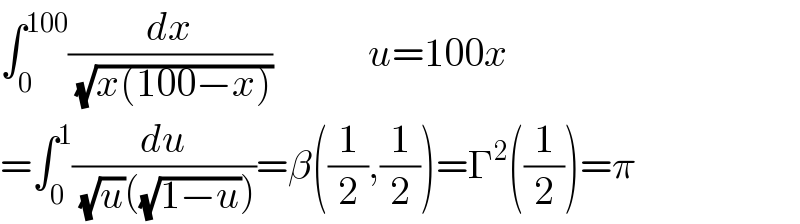
$$\int_{\mathrm{0}} ^{\mathrm{100}} \frac{{dx}}{\:\sqrt{{x}\left(\mathrm{100}−{x}\right)}}\:\:\:\:\:\:\:\:\:\:\:\:{u}=\mathrm{100}{x} \\ $$$$=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{du}}{\:\sqrt{{u}}\left(\sqrt{\mathrm{1}−{u}}\right)}=\beta\left(\frac{\mathrm{1}}{\mathrm{2}},\frac{\mathrm{1}}{\mathrm{2}}\right)=\Gamma^{\mathrm{2}} \left(\frac{\mathrm{1}}{\mathrm{2}}\right)=\pi \\ $$
