Menu Close

0-12-x-tanx-cotx-dx-

Tinku Tara 0 Comments
Pin




Question Number 154011 by mathdanisur last updated on 13/Sep/21
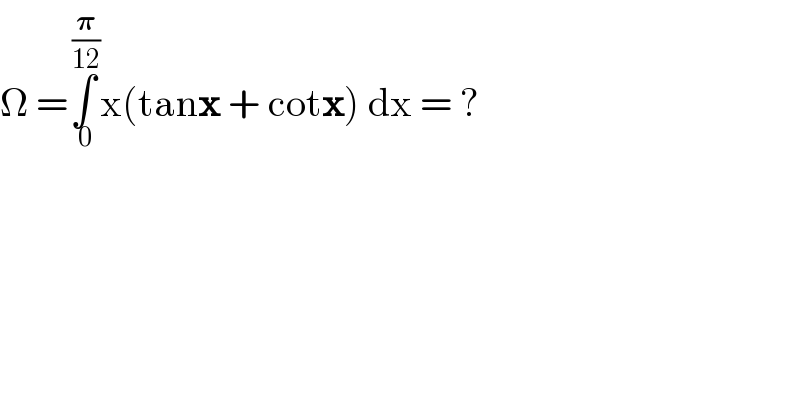
Ω =∫_( 0) ^( (𝛑/(12))) x(tanx + cotx) dx = ?
$$\Omega\:=\underset{\:\mathrm{0}} {\overset{\:\frac{\boldsymbol{\pi}}{\mathrm{12}}} {\int}}\mathrm{x}\left(\mathrm{tan}\boldsymbol{\mathrm{x}}\:+\:\mathrm{cot}\boldsymbol{\mathrm{x}}\right)\:\mathrm{dx}\:=\:? \\ $$
Commented by alisiao last updated on 13/Sep/21
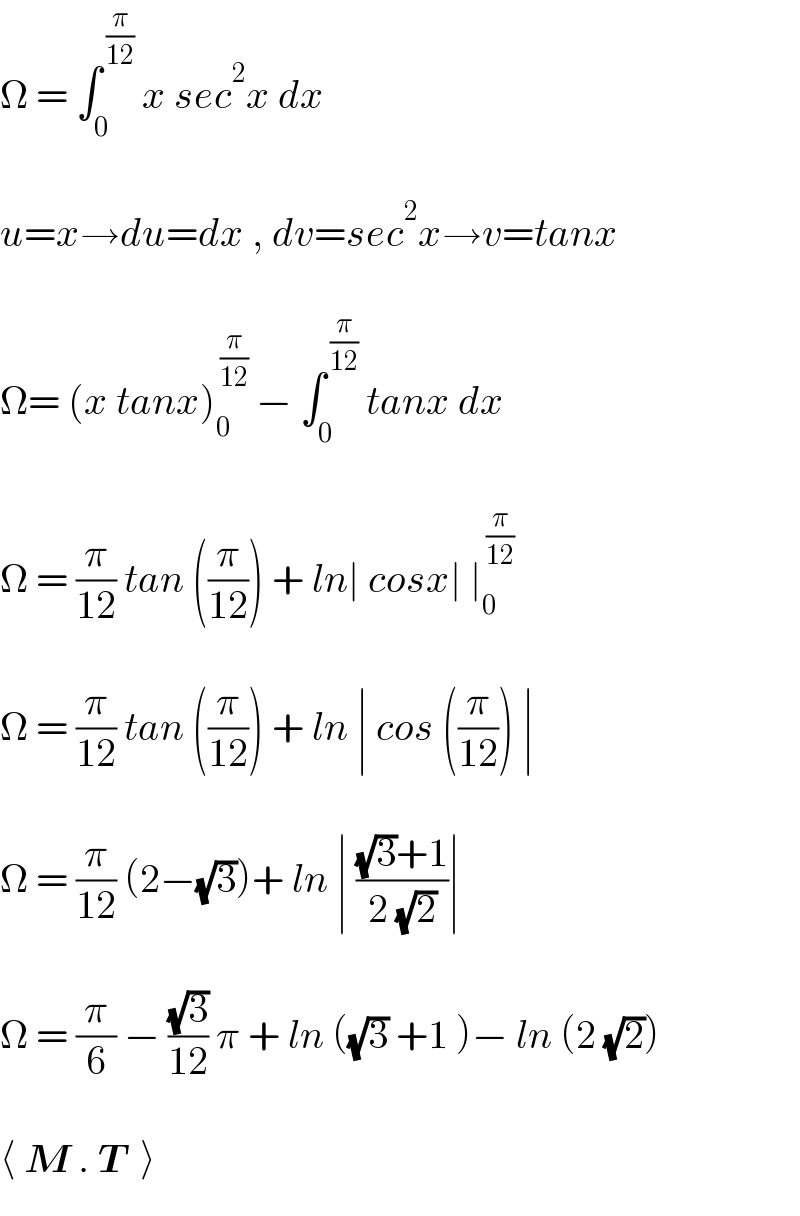
Ω = ∫_0 ^( (π/(12))) x sec^2 x dx u=x→du=dx , dv=sec^2 x→v=tanx Ω= (x tanx)_0 ^( (π/(12))) − ∫_0 ^( (π/(12))) tanx dx Ω = (π/(12)) tan ((π/(12))) + ln∣ cosx∣ ∣_0 ^( (π/(12))) Ω = (π/(12)) tan ((π/(12))) + ln ∣ cos ((π/(12))) ∣ Ω = (π/(12)) (2−(√3))+ ln ∣ (((√3)+1)/(2 (√2)))∣ Ω = (π/6) − ((√3)/(12)) π + ln ((√3) +1 )− ln (2 (√2)) ⟨ M . T ⟩
$$\Omega\:=\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{12}}} \:{x}\:{sec}^{\mathrm{2}} {x}\:{dx} \\ $$$$ \\ $$$${u}={x}\rightarrow{du}={dx}\:,\:{dv}={sec}^{\mathrm{2}} {x}\rightarrow{v}={tanx} \\ $$$$ \\ $$$$\Omega=\:\left({x}\:{tanx}\right)_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{12}}} \:−\:\int_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{12}}} \:{tanx}\:{dx} \\ $$$$ \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{12}}\:{tan}\:\left(\frac{\pi}{\mathrm{12}}\right)\:+\:{ln}\mid\:{cosx}\mid\:\mid_{\mathrm{0}} ^{\:\frac{\pi}{\mathrm{12}}} \\ $$$$ \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{12}}\:{tan}\:\left(\frac{\pi}{\mathrm{12}}\right)\:+\:{ln}\:\mid\:{cos}\:\left(\frac{\pi}{\mathrm{12}}\right)\:\mid \\ $$$$ \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{12}}\:\left(\mathrm{2}−\sqrt{\mathrm{3}}\right)+\:{ln}\:\mid\:\frac{\sqrt{\mathrm{3}}+\mathrm{1}}{\mathrm{2}\:\sqrt{\mathrm{2}}}\mid\: \\ $$$$ \\ $$$$\Omega\:=\:\frac{\pi}{\mathrm{6}}\:−\:\frac{\sqrt{\mathrm{3}}}{\mathrm{12}}\:\pi\:+\:{ln}\:\left(\sqrt{\mathrm{3}}\:+\mathrm{1}\:\right)−\:{ln}\:\left(\mathrm{2}\:\sqrt{\mathrm{2}}\right) \\ $$$$ \\ $$$$\langle\:\boldsymbol{{M}}\:.\:\boldsymbol{{T}}\:\:\rangle \\ $$
Commented by mathdanisur last updated on 13/Sep/21
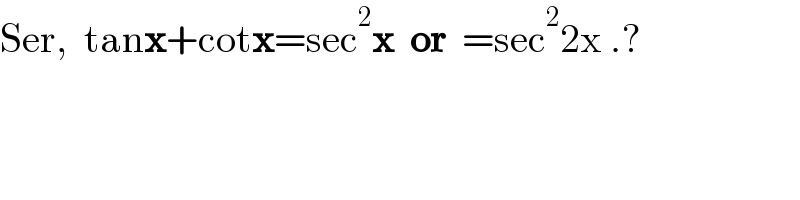
Ser, tanx+cotx=sec^2 x or =sec^2 2x .?
$$\mathrm{Ser},\:\:\mathrm{tan}\boldsymbol{\mathrm{x}}+\mathrm{cot}\boldsymbol{\mathrm{x}}=\mathrm{sec}^{\mathrm{2}} \boldsymbol{\mathrm{x}}\:\:\boldsymbol{\mathrm{or}}\:\:=\mathrm{sec}^{\mathrm{2}} \mathrm{2x}\:.? \\ $$
Commented by mnjuly1970 last updated on 13/Sep/21
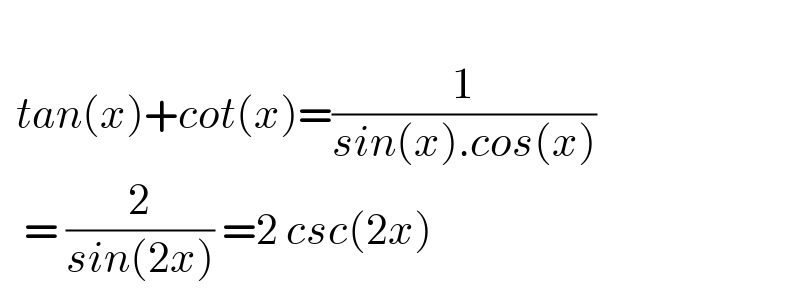
tan(x)+cot(x)=(1/(sin(x).cos(x))) = (2/(sin(2x))) =2 csc(2x)
$$ \\ $$$$\:\:{tan}\left({x}\right)+{cot}\left({x}\right)=\frac{\mathrm{1}}{{sin}\left({x}\right).{cos}\left({x}\right)} \\ $$$$\:\:\:=\:\frac{\mathrm{2}}{{sin}\left(\mathrm{2}{x}\right)}\:=\mathrm{2}\:{csc}\left(\mathrm{2}{x}\right)\: \\ $$
Commented by tabata last updated on 13/Sep/21
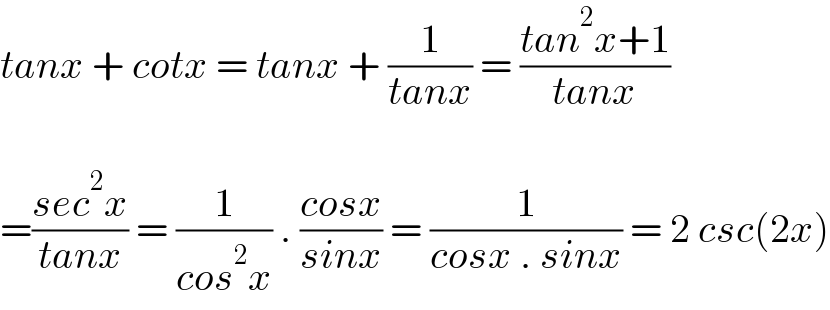
tanx + cotx = tanx + (1/(tanx)) = ((tan^2 x+1)/(tanx)) =((sec^2 x)/(tanx)) = (1/(cos^2 x)) . ((cosx)/(sinx)) = (1/(cosx . sinx)) = 2 csc(2x)
$${tanx}\:+\:{cotx}\:=\:{tanx}\:+\:\frac{\mathrm{1}}{{tanx}}\:=\:\frac{{tan}^{\mathrm{2}} {x}+\mathrm{1}}{{tanx}} \\ $$$$ \\ $$$$=\frac{{sec}^{\mathrm{2}} {x}}{{tanx}}\:=\:\frac{\mathrm{1}}{{cos}^{\mathrm{2}} {x}}\:.\:\frac{{cosx}}{{sinx}}\:=\:\frac{\mathrm{1}}{{cosx}\:.\:{sinx}}\:=\:\mathrm{2}\:{csc}\left(\mathrm{2}{x}\right) \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *